Функционально полные системы логических функций

Из множества функционально полных наборов рассмотрим только те, которые имеют наибольшее практическое значение.

1.5.1. Основная функционально полная система логических функций. Наибольшее распространение получил набор, в состав которого входят три логические функции:

· f₁₀ – инверсия (логическая связь НЕ, логическое отрицание);

· f₁ – конъюнкция (логическая связь И, логическое умножение),

· f₇ – дизъюнкция (логическая связь ИЛИ, логическое сложение).

Этот набор получил название функционально полной системы логических функций (ОФПС). Из теоремы о функциональной полноте следует, что основная функционально полная система логических функций является избыточной, так как условиям теоремы отвечают наборы функций f₁₀ и f₁ или f₁₀ и f₇. Свойства этих функций были рассмотрены ранее.

Из определения представления переключательной функции в виде дизъюнктивной или конъюнктивной нормальной формы следует, что эти представления реализуются в основной функционально полной системе логических функций.

1.5.2. Законы алгебры логики в ОФПС и их следствия. В алгебре логики имеются четыре основных за­кона, регламентирующих порядок производства операций НЕ, И, ИЛИ в любом логическом выражении:

· переместительный (коммутативный);

· сочетательный (ассоциативный);

· распределительный (дистрибутивный);

· инверсии (правило Де Моргана).

Переместительный закон. Этот закон справедлив как для дизъюнкции, так и для конъюнкции:

x₁ Úx₂ = x₂ Úx₁; x₁ Ùx₂ = x₂ Ù x₁. (5.1)

Справедливость выражения (5.1) нетрудно доказать простой подста­новкой в него различных значений x₁ и x₂. Поскольку любую переста­новку большего количества слагаемых можно свести к последователь­ности перестановок слагаемых в отдельных парах, то переместитель­ный закон будет справедлив при любом числе слагаемых.

Сочетательный закон. Этот закон, так же как и переместительный, является симметричным, т. е. справедливым и для дизъюнкции, и для конъюнкции:

x₁ Úx₂ Úx₃ = x₁Ú(x₂ Úx₃) = (x₁ Úx₂)Úx₃= x₂Ú(x₁ Úx₃); (5.2)

x₁ Ùx₂ Ùx₃ = x₁Ùx₂ Ùx₃) = (x₁ Ùx₂)Ùx₃= x₂Ù(x₁ Ùx₃).

Доказательство этого закона также не представляет никаких труд­ностей и может быть выполнено простой подстановкой.

Распределительный закон. В отличие от обычной алгебры алгебра логики симметрична. В ней справедливы два распределительных закона:

для логического умножения относительно логического сложения (рас­пределительный закон 1-го рода) и для логического сложения относи­тельно логического умножения (распределительный закон 2-го рода).

1. Распределительный закон 1-го рода записывается следующим образом:

(x₁Úx₂)Ùx₃=(x₁Ùx₃)Ú (x₂ Ùx₃). (5.3)

Справедливость формулы (5.3), а также и ее более общего случая, когда в скобках заключена сумма любого количества слагаемых, можно доказать путем установления идентичности условий обращения в 0 или 1 ее левой и правой частей. Условием обращения в нуль левой части выражения (5.3) состоит в том, чтобы нулю равнялся либо один аргумент х₃, либо одновременно аргументы x₁ и x₂. Условия обращения в нуль правой части выражения (5.1) такие же. Следовательно, распределительный закон 1-го рода справедлив для алгебры логики.

2. Распределительный закон 2-го рода имеет вид

(x₁Ùx₂)Úx₃=(x₁Úx₃)Ù (x₂Úx₃). (5.4)

Cправедливость формулы (5.4) (при любом количестве аргументов) нетрудно доказать посредством установления идентичности условий обращения обеих ее частей в единицу.

Закон инверсии (правило Де Моргана). Этот закон, так же как и все предыдущие, симметричен относительно логических сложения и умножения.

1. Отрицание логической суммы нескольких аргументов равно ло­гическому произведению отрицаний этих же аргументов:

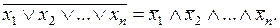(5.5)

Доказательство закона не представляет трудностей, поскольку условие обращения в нуль как левой, так и правой частей выражения (5.5) состоит в том, чтобы был истинным хотя бы один аргумент.

2. Отрицание логического произведения нескольких аргументов равно логической сумме отрицаний этих же аргументов:

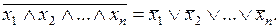(5.6)

Справедливость этого закона следует из того, что условие обращения в единицу обеих частей формулы (5.6) заключается в том, чтобы был ложным хотя бы один аргумент.

Следствия из законов алгебры логики. Из доказанных выше за­конов можно вывести ряд следствий, которые сформулируем в виде правил.

Правило выполнения совместных логических действий (правило старшинства логических функций).. При решении логических задач приходится встречаться с выражениями, содержащими действия отри­цания, конъюнкции и дизъюнкции в любом сочетании. По аналогии с арифметическими действиями будем считать отрицание логическим действием первой ступени (старшей логической опера­цией), конъюнкцию — действием второй ступени, а дизъюнкцию — действием третьей ступени (младшей логической операцией).

Старшинство операции инверсии вытекает из закона инверсии, в соот­ветствии с которым логическая сумма отрицаний некоторых аргументов не равна отрицанию их суммы (это справедливо и для логического произведения). Это значит, что ни операцию дизъюнкции, ни операцию конъюнкции нельзя проводить, игнорируя знак отрицания над каким-либо из логических аргументов, т. е. операцию отрицания надо про­водить в первую очередь.

Относительно операций логического сложения и умножения на основании симметричности законов алгебры логики можно сказать, что они «равноправны». Из этого следует, что можно условиться считать более старшей операцией любую из них, но, приняв какое-либо усло­вие, надо придерживаться его все время. На практике оказалось удоб­нее считать более старшей операцию логического умножения, так как это соответствует правилам обычной алгебры и для нас более привычно.

На основе изложенного можно сформулировать следующее пра­вило выполнения совместных логических действий: если в логическом выражении встречаются только действия одной и той же ступени, то их принято выполнять в том порядке, в котором они написаны; если в логическом выражении встречаются действия различных ступеней, то сначала принято выполнять действия первой ступени, затем — второй, и только после этого — третьей. Всякое отклонение от этого порядка должно быть обозначено скобками.

Правило склеивания. Прежде чем сформулировать само правило, введем некоторые новые понятия. Если имеется некоторый конечный набор логических аргументов x₁, x₂, … x_n, то логическое произведение любого их числа называется элементарным в том случае, когда сомножите­лями в нем являются либо одиночные аргументы, либо отрицания одиночных аргументов. Так, например, f₁(х₁, х₂, x₃, х₄) = х₁× х₂× x₃×х₄ — элементарное произведение (элементарная конъюнкция); 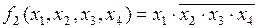— не является элементарным про­изведением.

Cимвол любого аргумента в элементарной конъюнк­ции может встречаться только один раз, поскольку произведение аргу­мента самого на себя равно этому же аргументу, а произведение аргу­мента на свое отрицание равно нулю. Количество сомножителей в элементарной конъюнкции называется ее рангом.

Два элементарных произведения одинакового ранга r называются соседними, если они являются функциями одних и тех же аргументов и отличаются только знаком отрицания (инверсии) одного из сомножи­телей. Например, элементарные конъюнкции

f₁(х₁, х₂, x₃, х₄) = х₁× х₂× x₃×х₄ и f₃(х₁, х₂, x₃, х₄) =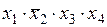

являются соседними, так как отличаются только одной инверсией в переменной x₂, а элементарные конъюнкции

f₃(х₁, х₂, x₃, х₄) = 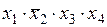и f₄(х₁, х₂, x₃, х₄) =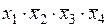

соседними не являются.

Правило склеивания для элементар­ных конъюнкций может быть сформулировано следующим образом: логическую сумму двух соседних произведений неко­торого ранга r можно заменить одним элементарным произведением ранга r-1, являющимся общей частью исходных слагаемых.

Это правило является следствием распределительного закона 1-го рода и доказывается путем вынесения за скобку общей части сла­гаемых, являющихся соседними конъюнкциями. Тогда в скобках ос­тается логическая сумма некоторого аргумента и его инверсии, равная единице, что и доказывает справедливость правила.

Например,

.

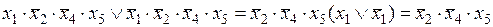Поскольку алгебра логики является симметричной, то все опреде­ления, данные для конъюнкции, будут справедливы и для дизъюнкции.

Если имеется некоторый конечный набор логических аргументов, то логическая сумма (дизъюнкция), зависящая от любого их числа, называется элементарной в том случае, когда слагаемыми в ней явля­ются либо одиночные аргументы, либо отрицания одиночных аргу­ментов.

Количество слагаемых в элементарной дизъюнкции называется ее рангом. Две элементарные суммы одинакового ранга называются соседними, если они являются функциями одних и тех же аргументов и отлича­ются только знаком отрицания (инверсии) одного из слагаемых.

Правило склеивания двух элементарных дизъюнкций формули­руется так: логическое произведение двух соседних сумм некоторого ранга r можно заменить одной элементарной суммой ранга r- 1, являющейся общей частью исходных сомножителей.

Это правило является следствием распределительного закона 2-го рода и применяется для упрощения логических выражений.

Например:

Правило поглощения. Так же как и склеивание, поглощение может быть двух видов. Правило поглощения для двух элементарных конъюнкций форму­лируется так: логическую сумму двух элементарных произведений раз­ных рангов, из которых одно является собственной частью другого, можно заменить слагаемым, имеющим меньший ранг.

Это правило является следствием распределительного закона 1-го рода. Доказывается оно посредством вынесения за скобку общей части слагаемых. В скобках останется логическая сумма некоторого выражения и единицы, равная в свою очередь также единице, что и до­казывает справедливость правила. Например,

Правило поглощения для двух элементарных дизъюнкций: логи­ческое произведение двух элементарных сумм разных рангов, из которых одна является общей частью другой, можно заменить сомножителем, имеющим меньший ранг.

Это правило является следствием распределительного закона 2-го рода и также находит широкое применение для упрощения логи­ческих функций.

Правило развертывания. Это правило регламентирует действие, обратное склеиванию. Иногда требуется представить некоторое логическое выражение в виде совокупности конституент единицы или конституент нуля. Если членами преобразуемого выражения являются элементарные конъюнкции, то переход от них к конституентам единицы производится в три этапа по следующему правилу:

· в развертываемую элементарную конъюнкцию ранга r в качестве дополнительных сомножителей вводится п-r единиц, где п — ранг конституенты;

· каждая единица представляется в виде логической суммы некото­рой, не имеющейся в исходной конъюнкции переменной и ее отрицания: ;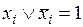

· производится раскрытие всех скобок на основе распределитель­ного закона первого рода, что приводит к развертыванию исходной элементарной конъюнкции ранга r в логическую сумму кон-ституент единицы.

Пример 5.1. Развернуть элементарную конъюнкцию f(x₁,x₂,x₃,x₄) = =x₁×x₃ в логичес­кую сумму конституент единицы.

Решение. Ранг конституенты единицы для данной функции равен 4. Произ­водим развертывание исходной конъюнкции поэтапно в соответствии с правилом развертывания:

1-й этап— f(x₁,x₂,x₃,x₄) = x₁×1×x₃×1.

2-й этап — f(x₁,x₂,x₃,x₄) =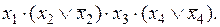

3-й этап — f(x₁,x₂,x₃,x₄)=

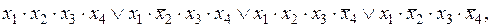= что и тре­бовалось получить.

Если членами преобразуемого выражения являются элементарные дизъюнкции, то переход от них к конституентам нуля производится также в три этапа по следующему правилу:

· в развертываемую элементарную дизъюнкцию ранга r в качестве дополнительных слагаемых вводится п-r нулей;

· каждый нуль представляется в виде логического произведения некоторой, не имеющейся в исходной дизъюнкции переменной, и ее отри­цания:

· получившееся выражение преобразуется на основе распределитель­ного закона второго рода таким образом, чтобы произвести раз­вертывание исходной элементарной дизъюнкции ранга r в логическое произведение конституент нуля.

Пример 5.2. Развернуть элементарную дизъюнкцию f(x₁,x₂,x₃,x₄)= =x₃Úx₄ в логическое произведение конституент нуля.

Решение. Ранг конституенты нуля п = 4. Далее производим развертывание исходной дизъюнкции поэтапно в соответствии с правилом развер­тывания:

1-й этап — f(x₁,x₂,x₃,x₄) =0Ú0Úx₃Úx₄;

2-й этап — f(x₁,x₂,x₃,x₄) =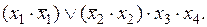

3-йэтап—f(x₁,x₂,x₃,x₄)=

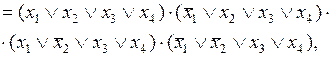
что и требовалось получить.

Проверить правильность проведенных преобразований можно при помощи пра­вила склеивания.

1.5.3. Функционально полные системы логических функций. Анализ принадлежности переключательных функций замкнутым классам показывает, что существуют две переключательные функции f₈ и f₁₄, не принадлежащие ни одному классу. Согласно теореме о функциональной полноте, каждая из этих функций образует функционально полную систему логических связей и используя только одну из них можно представить любую, сколь угодно сложную переключательную функцию.

Операция Пирса (стрелка Пирса) реализует функцию, которая принимает значение, равное единице только в том случае, когда все ее аргументы равны 0 (ИЛИ-НЕ), что может быть записано в ОФПС для функции двух переменных следующим образом:

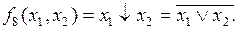(5.7)

Используя операции суперпозиции и подстановки можно показать, что операция Пирса может быть реализована для n аргументов:

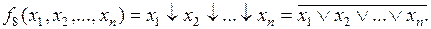(5.8)

Для представления переключательной функции в базисе Пирса необходимо выполнить следующие действия:

· представить переключательную функцию f в конъюнктивной нормальной форме;

· полученное выражение представить в виде 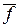(поставить два знака отрицания);

· применить правило Де Моргана.

Например, для того чтобы представить функцию

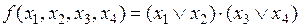
в базисе Пирса, необходимо выполнить следующие преобразования:

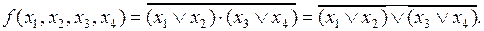
Для представления полученного выражения в базисе Пирса воспользуемся соотношением (5.7):

.

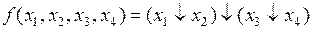Операция Шеффера (штрих Шеффера) реализует функцию, которая принимает значение, равное нулю, только в том случае, когда все ее аргументы равны 1 (И-НЕ), что может быть записано в ОФПС для функции двух переменных следующим образом:

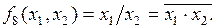(5.9)

Используя операции суперпозиции и подстановки, можно показать, что операция Пирса может быть реализована для n аргументов:

f(x₁,x₂,…,x_n)= x₁½x₂½…½x_n =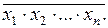 (5.10)

Для представления переключательной функции в базисе Шеффера необходимо выполнить следующие действия:

· представить переключательную функцию f в дизъюнктивной нормальной форме;

· полученное выражение представить в виде 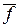(поставить два знака отрицания);

· применить правило Де Моргана.

Например, для того чтобы представить функцию

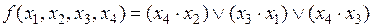
в базисе Шеффера, необходимо выполнить следующие преобразования:

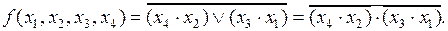
Для представления полученного выражения в базисе Шеффера воспользуемся соотношением (5.9):

f(x₁,x₂,x₃,x₄)=(x₄½x₂)½(x₃½x₁).

2. МИНИМИЗАЦИЯ ПЕРЕКЛЮЧАТЕЛЬНЫХ ФУНКЦИЙ

2.1. Вхождение функции в функцию. Импликанты

Понятием "минимизация переключательных функций" объединяется ряд процедур, выполнение которых направлено на получение наиболее компактной, минимальной в некотором смысле формы представления переключательной функции. Как правило, в качестве критерия минимальности переключательной функции используется число букв в логическом выражении. Действительно, любые две рядом стоящие буквы связаны между собой знаком какой-либо логической операции. Поэтому, чем меньше букв в логическом выражении, тем меньше логических операций необходимо для реализации этого выражения, тем меньше логических элементов требуется для построения соответствующей комбинационной схемы. Это ведет к минимуму веса устройства, минимуму стоимости и т.д.

Как правило, все алгоритмы минимизации начинаются с приведения переключательной функции к канонической форме, в качестве которой используются совершенные дизъюнктивная и конъюнктивная нормальные формы. Основные этапы минимизации приведены на рис. 2.1.

Смысл минимизации переключательных функций заключается в поиске совокупности таких элементарных конъюнкций (дизъюнкций), которые своими единицами (нулями) накрывали бы как можно большее число единиц (нулей) среди значений заданной переключательной функции.

Понятие вхождения одной переключательной функции в другую является весьма существенным, поскольку именно оно во многом определяет "механизм" минимизации переключательных функций.

Будем говорить, что переключательная функция j(х ₁, х ₂, …, х_n) входит в переключательную функцию f (х ₁, х ₂, …, х_n), если функция j накрывает своими нулями все нули функции f, а единицы функции f накрываются как нулями, так и единицами функции j; т.е. функция j должна иметь нулевых значений не меньше, чем функция f, и, кроме того, нули функции j должны быть определенным образом расположены.

Дата добавления: 2014-01-06