Основные понятия и определения теории графов

Теорема 2.7.1. Минимальная ДНФ неполностью определенной функ­ции f(x1, x2, …, xn) совпадает с дизъюнкцией самых коротких импликант экви­ва­лент­ной функции j1(x1, x2, …, xn), которые совместно поглощают все консти­туенты единицы функции j0(x1, x2, …, xn) и ни одна из которых не является лишней.

Определение 2.7.1. Пусть переключательная функция f(x1, x2, …, xn) не опре­де­лена на p наборах аргументов. Тогда полностью определенную функцию j(x1, x2, …, xn) будем называть эквивалентной функции f(x1, x2, …, xn), если ее значения совпадают со значениями функции f(x1, x2, …, xn) на тех наборах, на которых эта функция f определена.

Существует 2 ^p вариантов выбора значений функции на запрещенных на­бо­рах и, следовательно, 2 ^р различных переключательных функций, эквива­лент­ных функции f (x ₁, x ₂, …, x_n). Поэтому задача минимизации неполностью определенной функции f (x ₁, x ₂, …, x_n) сводится к отысканию такой экви­ва­лентной функции j (x ₁, x ₂, …, x_n), которая имеет простейшую минимальную форму.

Введем эквивалентные функции j ₀(x ₁, x ₂, …, x_n) и j ₁(x ₁, x ₂, …, x_n), значения которых на всех запрещенных наборах функции f (x ₁, x ₂, …, x_n) равны, соответственно, нулю и единице.

Для доказательства теоремы рассмотрим СДНФ некоторой эквива­лент­ной функции j_i (x ₁, x ₂, …, x_n). Конституенты единицы, входящие в эту форму, обязательно войдут и в СДНФ функции j ₁(x ₁, x ₂, …, x_n). Поэтому любая простая импликанта функции j_i (x ₁, x ₂, …, x_n) будет совпадать с импликантой функции j ₁(x ₁, x ₂, …, x_n) или будет поглощаться ею. Другими словами, среди импликант функции j ₁(x ₁, x ₂, …, x_n) всегда найдется такая, которая по­гло­щает любую импликанту любой эквивалентной функции j_i (x ₁, x ₂, …, x_n). Следовательно, самыми короткими произведениями, накрывающими единицы функции f (x ₁, x ₂, …, x_n), будут импликанты j ₁(x ₁, x ₂, …, x_n).

Среди всех ПФ, эквивалентных заданной, функция j ₀(x ₁, x ₂, …, x_n) имеет минимальное количество конституент единицы. Следовательно, и количество простых импликант [из набора импликант функции j ₁(x ₁, x ₂, …, x_n)], необходимых для поглощения конституент функции j ₀(x ₁, x ₂, …, x_n), будет минимальным. Если составить дизъюнкции наиболее коротких импликант функции j ₀(x ₁, x ₂, …, x_n), которые совместно накрывают все конституенты единицы функции j ₀(x ₁, x ₂, …, x_n), то получим, очевидно, минимальную форму представления функции f (x ₁, x ₂, …, x_n).

Ввиду того, что для накрытия единиц функции j ₀(x ₁, x ₂, …, x_n) выби­раются импликанты другой функции, дизъюнкция этих импликант не равняется функции j ₀(x ₁, x ₂, …, x_n). Однако, такая дизъюнкция обязательно равна одной из функций, эквивалентных функции f (x ₁, x ₂, …, x_n).

Пример. Найти минимальную дизъюнктивную нормальную форму ПФ, заданной таблицей.

x 1

x 2

x 3

x 4

f (x 1, x 2, x 3, x 4)

Полагая, что пустые клетки заполнены нулями, найдем СДНФ экви­ва­лентной функции j ₀(x ₁, x ₂, x ₃, x ₄):

.

СНДФ функции j ₁(x ₁, x ₂, …, x_n), полученная после заполнения пустых клеток таблицы единицами, будет

Выполнив операции склеивания и поглощения, получим сокращенную ДНФ функции j ₁ (x ₁, x ₂, x ₃, x ₄), в которую войдут все ее простые импликанты:

Составим импликантную матрицу, включив в нее конституенты единицы функции j ₀(x ₁, x ₂, x ₃, x ₄) и импликанты функции j ₁(x ₁, x ₂, x ₃, x ₄).

Импли- канты	Конституенты
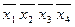
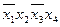
				x 1 x 2 x 3 x 4
x 1 x 2				x	x
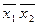
	x
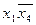
			x	x
	x		x
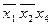
		x
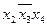
		x

Импликанта x ₁ x ₂ обязательно должна входить в мин ДНФ, т.к. только она поглощает конституенту x ₁ x ₂ x ₃ x ₄. Импликанты x ₁ x ₂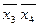совместно накрывают все конституенты, кроме 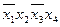; последняя может быть накрыта импликантам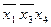и или 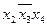. Поэтому минимальные ДНФ функции f (x ₁, x ₂, x ₃, x ₄) будут:

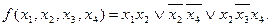
Пример. Найти минимальную ДНФ функции f (x ₁, x ₂, x ₃, x ₄), эквивалентая функция j ₀(x ₁, x ₂, x ₃, x ₄) которой имеет вид:

а комбинации 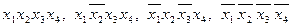являются запрещен­ными.

Эквивалентную функцию j ₁(x ₁, x ₂, …, x_n) можно получить, добавив к СДНФ функции j ₁(x ₁, x ₂, …, x_n) запрещенные комбинации переменных:

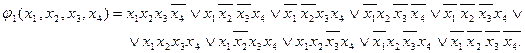
Проведя операции склеивания и поглощения, найдем простые импли­кан­ты функции j ₁(x ₁, x ₂, x ₃, x ₄); x ₁ x ₂ x ₃, x ₁ x ₃ x ₄, 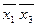, 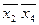. Импликантная матрица функции f (x ₁, x ₂, x ₃, x ₄) имеет вид.

Импли- канты	Конституенты
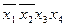
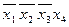
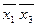
				x	x
		х	х		х
x 1 x 2 x 3	х
x 1 x 3 x 4

Функция f (x ₁, x ₂, x ₃, x ₄) имеет единственную минимальную ДНФ

В нижней строке импликантной матрицы крестики отсутствуют и, сле­до­вательно, импликанта x ₁ x ₃ x ₄ не поглощает ни одну из конституент единицы функции j ₀(x ₁, x ₂, x ₃, x ₄). Это связано с тем, что данная импликанта обра­зо­валась в результате склеивания конституент функции j ₁(x ₁, x ₂, x ₃, x ₄), которые в функцию j ₀(x ₁, x ₂, x ₃, x ₄) не входят.

Чтобы найти простейшее представление неполностью определенной ПФ, кроме минимальных дизъюнктивных форм следует получить минималь­ные конъюнктивные нормальные формы и выбрать из них ту, которая содержит наименьшее число букв.

Алгоритм получения минимальных конъюнктивных форм подобен рас­смот­ренному алгоритму получения минимальной ДНФ и заключается в следующем.

Пусть задана неполностью определенная функция f (x ₁, x ₂, …, x_n). Тогда для получения минимальной КНФ достаточно найти сокращенную КНФ эквивалентной функции j ₀(x ₁, x ₂, …, x_n), а функцию j ₁(x ₁, x ₂, …, x_n) записать в СКНФ. Затем следует составить ипликантную матрицу, включив в нее все конституенты нуля функции j ₁(x ₁, x ₂, …, x_n) и все члены сокращенной конъюнктивной нормальной формы функции j ₀(x ₁, x ₂, …, x_n). По импли­кант­ной матрице рассмотренным выше способом можно получить минимальные КНФ функции f (x ₁, x ₂, …, x_n).

Пример. Найти минимальную КНФ функции, записанной таблицей.

x 1

x 2

x 3

x 4

f (x 1, x 2, x 3, x 4)

СКНФ эквивалентной функции j₁(x ₁, x ₂, x ₃, x ₄):

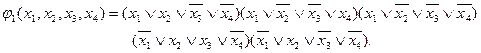
СКНФ функции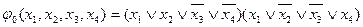

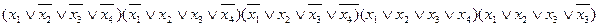
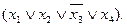
Сокращенная КНФ функции j ₀(x ₁, x ₂, x ₃, x ₄)

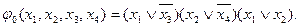
Импликантная матрица имеет вид:

Импли- канты
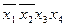
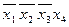
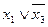
	х	х	х
	х			х	х
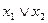
	х

Минимальная КНФ функции f (x ₁, x ₂, x ₃, x ₄)

Рассмотренная функция имеет четыре минимальные ДНФ

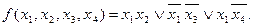
Здесь больше букв, чем в МКНФ.

При использовании понятия «граф» в математике чаще всего имеют в виду графическое определение (задание) связей между объектами произ­воль­ной природы. Можно говорить о графической форме представления процесса перехода цифрового автомата из одного состояния в другое, о графическом способе задания связей между атомами в молекуле вещества, о графическом представлении последовательности встреч команд при проведении спортивных соревнований и т.д. Математический аппарат теории графов является эффективным инструментом построения и исследования дискрет­ных моделей и систем различной природы.

Граф может интерпретироваться либо как некоторая геометрическая фи­гу­ра в пространстве, состоящая из точек и соединяющих их линий, либо как некоторый теоретико-множественный объект. Поэтому многочисленные оп­ре­деления понятия «граф» могут иметь либо геометрический, либо достаточ­но абстрактный теоретико-множественный смысл.

Определение 1.1. Множество X ={ x ₁, x ₂, …, x_k, …} и набор E пар объектов ви­да { x_i, x_j } или (x_i, x_j) из множества X называется графом. Будем обозначать граф символом G.

Множество X объектов будем называть множеством вершин графа, а эле­менты множества E, т.е. множества пар вида { x_i, x_j } или (x_i, x_j), соот­ветственно ребрами или дугами. Отдельное ребро графа G, например e_k Î E, будем обозначать парой { x_l, x_m }, т.е. e_k= { x_l, x_m }. Использование фигурных скобок в данном случае означает, что пара { x_l, x_m } является неупорядоченной, т.е. роли не играет, какая из вершин в паре является начальной, а какая ко­нечной. Если же в некоторой паре вершин, например (x_p, x_q), указаны на­чальная и конечная вершины, то говорят, что эта совокупность вершин определяет дугу графа. Таким образом, ребро – это неупорядоченная, а дуга – упорядоченная пара вершин. Возможны случаи, когда начальная и конечная вершины ребра (или дуги) совпадают, в этом случае говорят, что в графе имеется петля, например, { x_n, x_n }.

Граф, состоящий из вершин и соединяющих их ребер, называется неори­ен­тированным, а граф, состоящий из вершин и соединяющих их дуг, – ориен­тированным, или кратко орграфом. Графы, содержащие как ребра, так и дуги, именуются смешанными.

Таким образом, граф G определяется множеством своих вершин X, мно­жеством ребер или дуг E и может обозначаться символами G (X, E). Однако в этом обозначении нет прямых указаний на то, какие вершины графа G связаны между собой какими именно ребрами.

Приведенное выше определение понятия «граф» в значительной степени является абстрактным, и поэтому для введения других понятий и определений целесообразно иметь геометрическую интерпретацию понятия «граф», яв­ляю­щуюся более наглядной. С этой целью будем рассматривать в евклидо­вом пространстве определенного вида геометрические фигуры w, состоящие из точек b ₁, b ₂, …, b_k, …, также именуемых вершинами, и линий, являю­щихся либо дугами окружностей, либо отрезками прямых; каждая из этих линий объединяет вершины в пары, например, { b _i, b_j } или (b_l, b_m); возможны вырожденные ситуации, когда b_i = b_j, что соответствует уже рассмотренному понятию петли.

В связи с использованием геометрической интерпретации графа необхо­димо обратить внимание на следующие ограничения, которые, в частности, порождают вопросы о возможности реализации графов в прост­ранстве той или иной размерности (в трехмерном пространстве, на плос­кости).

1. Любая замкнутая кривая линия, т.е. e_i Î E, содержит одну и только од­ну точку из множества X (рис. 1.1, а).

2. Каждая разомкнутая линия e_j Î E содержит ровно две точки x_l, x_m Î X, являющиеся ее концами (рис. 1.1, б).

3. Линии e_i Î E и e_j Î E не могут иметь общих точек, которые не принад­лежали бы множеству X (рис. 1.1, в).

Таким образом, геометрический граф представляет собой фигуру в ев­кли­довом пространстве, которая состоит из множества точек и соединяющих их множества простых кривых, т.е. линий, не имеющих точек самопе­ре­сечения.

Между графом, интерпретируемым в теоретико-множественном смысле, и его геометрической реализацией существует взаимно однозначное соответ­ствие. Назовем фигуру w геометрической реализацией графа G, если уста­нов­лено взаимно однозначное соответствие между точками – вершинами фи­гу­ры w и вершинами графа G, а также между линиями, соединяющими вер­шины фигуры w, и ребрами графа G, причем такое, что если (b_ni, b_ng)«(x_i, x_j), то b_ni «x_i, b_nj «x_j, т.е. соответствующие кривые и ребра w и G соединяют соответствующие вершины.

На рис. 1.2 представлена геометрическая реализация графа, имеющего четыре вершины X ={ x ₁, x ₂, x ₃, x ₄} и шесть ребер E ={ e ₁, e ₂, e ₃, e ₄, e ₅, e ₆}, причем e ₁={ x ₁, x ₁}, e ₂={ x ₁, x ₂}, e ₃={ x ₂, x ₃}, e ₄={ x ₁, x ₃}, e ₅={ x ₁, x ₃} и e ₆={ x ₄, x ₄}. Если ребро e Î E геометрической реализации графа G (X, E) имеет своими концами вершины x_i и x_j, то говорят, что это ребро соединяет вершины x_i и x_j, т.е. e =(x_i, x_j); на рис. 1.2 петлями являются ребра e ₁ и e ₆. Пара (или большее число) ребер, соединяющих одни и те же вершины, например x_i и x_j, являются параллельными и называются кратными. На рис. 1.2 параллельными являются ребра e ₄ и e ₅. Вершины x_i и x_j геометрической реализации графа G (X, E), соединенные между собой хотя бы одним ребром, называются смежными. На рис. 1.2 смежными являются вершины x ₁ и x ₂, x ₁ и x ₃, x ₂ и x ₃. Вершина графа, не смежная ни с какой другой вершиной этого графа (возможно, кроме себя самой), называется изолированной; изолированной является вершина x ₄ на рис. 1.2.

Рис. 1.1

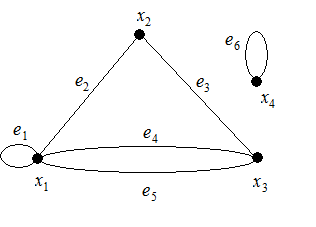
Рис. 1.2

Рис. 1.3

Аналогично два ребра геометрической реализации графа, имеющие хотя бы один общий конец (общую вершину), называются смежными. Смежными ребрами графа на рис. 1.2 являются, например, ребра e ₂ и e ₃, e ₁ и e ₅, e ₃ и e ₅ и т.д. Естественно, смежными являются параллельные ребра.

Таким образом, на множествах вершин X и ребер E неориентированного графа могут быть заданы отношения смежности.

Кроме отношения смежности, относящегося к элементам одного мно­жест­ва (например, множества вершин или множества ребер), может быть определено отображение инцидентности, относящееся к элементам различ­ных множеств. Если ребро e_k Î E геометрической реализации графа G (X, E) соединяет вершины x_i и x_j, x_i, x_j Î X, т.е. e_k =(x_i, x_j), то говорят, что ребро e_k инцидентно вершинам x_i и x_j или вершины x_i и x_j инцидентны ребру e_k.

Таким образом, на множествах вершин X и ребер E графа может быть задано отображение инцидентности.

Следовательно, задать граф можно, указав множества его вершин X и ре­бер E и определив отношение смежности или отображение инцидентности Ф, т.е. G (X, E, Ф). В этом случае граф оказывается полностью определенным: символ Ф соответствует информации о том, какими ребрами соединены меж­ду собой какие вершины графа.

От неориентированного графа можно перейти к графу ориентирован­но­му, если на каждом ребре однозначно указать направление (например стрел­кой). Две дуги орграфа G (X, E, Ф), например e ₁ и e ₂, называются параллель­ными (или строго параллельными), если они инцидентны одним и тем же вершинам x_i и x_j, при этом e ₁=(x_i, x_j) и e ₂=(x_i, x_j). Если же e ₁=(x_i, x_j) и e ₂=(x_j, x_i), то дуги e ₁ и e ₂ называются антипараллельными. Петли могут быть ориенти­ро­ваны либо по часовой стрелке, либо против; однако ориентацию петли можно и не учитывать.

На основе рассмотренных понятий можно дать окончательные определе­ния неориентированного и ориентированного графов.

Назовем абстрактным неориентированным графом G (X, E, Ф) совокуп­ность непустого множества X, произвольного множества E, причем X Ç E =Æ, и произвольного отображения Ф: E ® X & X. Элементы множеств X и E - соответ­ственно вершины и ребра графа, а Ф – отображение инцидентности (отноше­ние смежности). Неупорядоченные пары вершин могут обозначаться сим­волами x_i & x_j.

Абстрактный ориентированный граф (орграф) G (X, E, Ф) представляет собой совокупность непустого множества X, произвольного множества E, причем такого, что 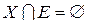, и произвольного отображения Ф: E ® X ´ X; эле­мен­ты множеств X и E являются соответственно вершинами и дугами графа G, а Ф – отображение инцидентности (отношение смежности). Симво­лом x_i x x_j обозначены упорядоченные пары вершин.

Рассмотрим произвольный неориентированный граф, например тот, который показан на рис. 1.2, и выделим некоторую его вершину. Число ребер неориентированного графа G (X, E, Ф), инцидентных вершине x_i (петля при этом учитывается дважды), называется степенью, или порядком этой вершины. Степень вершины можно обозначать символом d(x_i). Для вершины x ₁ графа, показанного на рис. 1.2, d(x ₁)=5, для x ₂ d(x ₂)=2, для x ₃ d(x ₃)=3, а для изолированной вершины x ₄ d(x ₄)=2.

Пусть G (X, E, Ф) – ориентированный граф. Если обозначить символом множество дуг, входящих в вершину x_i, а символом - множество дуг, выходящих из этой вершины, то тогда число 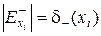будет называться полустепенью входа (захода) этой вершины, а число - полусте­пенью выхода (исхода) вершины x_i. Для вершины х ₅, показанной на рис. 1.3, , а .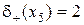

В заключение этого раздела рассмотрим две теоремы, связанные с понятием степени (порядка) вершин неориентированного графа.

Теорема 1.1. Сумма степеней вершин неориентированного графа G (X, E, Ф) рав­на удвоенному числу его ребер, т.е. если

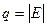, то .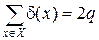

Это утверждение почти очевидно и следует из того, что каждое ребро графа инцидентно ровно двум вершинами, и поэтому вклад каждого ребра в сумму степеней вершин равен двум.

Теорема 1.2. В неориентированном графе G (X, E, Ф) число вершин нечет­ной степени четно.

Для доказательства этого утверждения разобьем множество вершин X графа на два подмножества X ₀ и X ₁, , причем Х ₀ и Х ₁ – со­от­вет­ственно множества вершин графа, имеющих четные и нечетные степени. С учетом Теоремы 1.1 можно записать

.

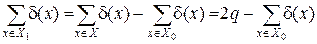В правой части этого выражения – разность двух целых четных чисел, поэтому и должна быть величиной четной. Но это может быть только в том случае, если и 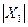четно.

Граф G ´(X ´, E ´) является частью графа G (X, E), если X ´Ì E и E ´Ì E, т.е. исходный граф содержит все вершины и ребра его части. Часть графа, которая наряду с некоторым подмножеством ребер (дуг) графа содержит и все инцидентные им вершины, называется подграфом. Часть графа, которая наряду с некоторым подмножеством ребер (дуг) графа содержит и все вер­шины исходного графа (X ´= X, E ´Ì E), называется суграфом. Рассмот­рен­ные графы показаны на рис. 1.4.

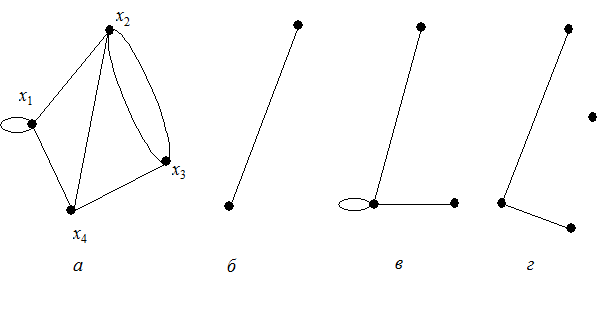
Рис.1.4

Исходный граф по отношению к его подграфу называется надграфом, а по отношению к суграфу – сверхграфом. Совокупность всех ребер (дуг) гра­фа, не принадлежащих его подграфу, вместе с инцидентными им вершинами об­разует дополнение подграфа. Говорят, что подграфы G ´ (X ´, E ´) и G "(X ", E ") разделены ребрами (дугами), если они не имеют общих ребер (дуг) (т.е. E ´Ç E "=Æ), и разделены вершинами, если у них нет общих вершин .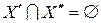

Графы G (X, E, Ф) и G ´ (X ´, E ´, Ф ´) называются изоморфными, если X = X ´, E = E ´ и существует взаимно однозначное соответствие между их вершинами и ребрами, причем такое, что соответствующие вершины соединяются соответ­ствующими ребрами. Для изоморфных графов G и G ´ должны суще­ствовать такие нумерации их вершин и ребер, при которых одноименные вершины оказываются соединенными одноименными ребрами. С точки зрения понятия изоморфизма абстрактный граф и его геометрическая реализация оказываются изоморфными. Поэтому в соответствии с уже доказанной теоремой о реализуемости любого конечного графа в простран­стве E ³ вместо абстрактных конечных графов можно рассматривать их гео­мет­ри­ческие реализации. Другими словами, с графами можно выполнять операции, как с геометрическими объектами. На рис. 1.5 представлены изоморфные, а на рис. 1.6 – неизоморфные графы.

Рис. 1.5

Рис. 1.6

Отношение изоморфизма графов является отношением эквивалентности, т.к. оно симметрично, транзитивно и рефлексивно. Поэтому множество всех графов можно разбить на классы так, что графы из одного класса попарно изоморфны, а графы из разных классов не изоморфны. Изоморфные графы естественно считать совпадающими, и их можно изображать одним рисунком. Изоморфные графы могут различаться природой своих элементов, но при использовании понятия «граф» конкретная природа его вершин, ребер или дуг во внимание не принимается.

В некоторых случаях необходимо различать изоморфные графы, в связи с чем вводится понятие «помеченного графа». Граф с n вершинами назы­вается помеченным, если его вершинам присвоены некоторые метки, например, номера 1, 2, …, n.

Введем операцию подразделения ребра графа G (X, E). Пусть { x_i, x_j } – произвольное ребро этого графа и y – некоторый объект, не принадлежащий множеству X. Операция подразделения ребра { x_i, x_j } графа заключается в построении графа G ´, множество вершин которого X ´= X È{ y }, а множество ребер E ´ содержит все ребра исходного графа, за исключением выделенного ребра { x_i, x_j }, и два дополнительных новых ребра:

.

Граф G ₂ называется подразделением графа G ₁, если он может быть получен из графа G ₁ путем применения конечного числа операций подразделения ребер.

Графы G ₁ и G ₂ называются гомеоморфными, если существуют такие их подразделения, которые изоморфны. Другими словами, два графа гомео­морфны, если они изоморфны с точностью до вершин второй степени (второго порядка). На рис. 1.7 показаны гомеоморфные графы. Изоморфизм графа G (X, E, Ф) на себя называется автоморфизмом этого графа. Автомор­физм обладает теми же свойствами, что и изоморфизм.

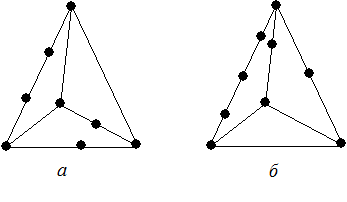
Рис. 1.7

2. ТИПЫ ГРАФОВ

В п. 1 уже были определены графы неориентированные, ориентирован­ные и смешанные.

Граф G (X, E, Ф) назовем конечным, если конечны множества его вершин X, а также ребер (или дуг) E.

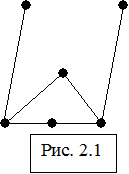Назовем граф обыкновенным, если в нем отсут­ствуют петли и парал­лель­ные ребра (дуги) (рис. 2.1). Граф, имеющий параллельные ребра (дуги), называется мультиграфом, а граф, в котором есть хотя бы одна петля, называется псевдографом (рис. 2.2 и 2.3). Если граф состоит только из изолированных вершин, то он именуется тривиальным; тривиальный граф без петель называется нуль-графом (рис. 2.4 и 2.5).

Если в обыкновенном неориентированном графе любые две вершины смежны, то такой граф именуется полным. Обыкновенный орграф называ­ет­ся полным, если для любых его вершин x и y существуют дуги e_i и e_j, такие, что e_i =(x, y) и e_j =(y, x). Если в каждую вершину полного графа добавить по петле, то получившийся граф будет называться насыщенным. На рис. 2.6, 2.7 и 2.8 показаны соответственно полные неориентированный, ориентирован­ный и насыщенный графы.

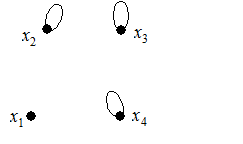
Рис. 2.2. Рис. 2.3 Рис. 2.4.

Рис. 2.5 Рис. 2.6

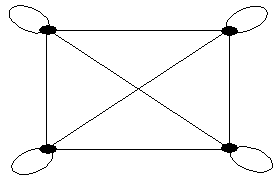
Рис. 2.6 Рис. 2.7

Граф G (X, E, Ф) называется двудольным (или биграфом), если множест­во его вершин может быть разбито на два непересекающихся подмножества X ₁ и X ₂, причем X = X ₁È X ₂, таким образом, что каждое ребро графа имеет одну инцидентную ей вершину во множестве X ₁, а другую – во множестве X ₂. На рис. 2.9 показан двудольный граф. Чтобы подчеркнуть отмеченную особен­ность двудольных графов, их изображают, размещая множества вершин X ₁ и X ₂ либо в разных строках, либо в разных столбцах.

В общем случае граф называется k -дольным, если множество его вершин можно разбить на k непересекающихся подмножеств X ₁, X ₂, …, X_k так, что не будет ребер, соединяющих вершины одного и того же подмножества.

Граф, степени всех вершин которого одинаковы и равны r, называется однородным (регулярным) графом степени r. Полный граф с n вершинами всегда является однородным графом степени n -1. Граф третьей степени называют кубическим; этот граф обладает рядом интересных свойств и, в частности, он всегда имеет четное число вершин. Можно выделить опре­деленные классы графов, исследуя возможность их реализации в простран­стве той или иной мерности.

Будем говорить, что граф G (X, E, Ф) укладывается на поверхности S, если его можно так нарисовать на этой поверхности, что никакие два его ребра не пересекались бы. Другими словами граф реализован на некоторой поверхности, если все его вершины и все внутренние точки ребер или дуг принадлежат этой поверхности.

Теорема 2.1. Каждый конечный граф G (X, E, Ф) может быть реализован в трехмерном евклидовом пространстве.

Доказательство. Пусть рассматриваемый граф содержит m вершин и n ребер (или дуг), т.е. и 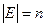. Выберем произвольную прямую и на ней разместим m точек – b ₁, b ₂, …, b_m, поставив их во взаимно однозначное соот­вет­ствие вершинам графа x ₁, x ₂, …, x_m. Затем через выбранную прямую проведем пучок из n полуплоскостей, поставив в соответствие ребра графа G (X, E, Ф) и плоскости из пучка. Пусть 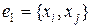. В полуплоскости, соответ­ствую­щей ребру e ₁, соединим точки b_i и b_j (вершины x_i и x_j графа) дугой окружности. Выполнив такое построение для всех остальных ребер графа в соответствующих полуплоскостях, получим в трехмерном евклидовом пространстве фигуру w, являющуюся геометрической реализацией графа G (X, E, Ф). Это и доказывает теорему, так как граф и его геометрическая реали­зация оказываются изоморфными.

Приведенная теорема не допускает понижения резмерности евклидова пространства, в котором мог бы быть реализован любой степени сложности конечный граф. Однако существует класс графов, реализуемых в прост­ранстве E ². Граф, реализуемый в пространстве E ², называется планарным. Если граф реализован на плоскости, то все его вершины и все внутренние точки его ребер или дуг принадлежат этой плоскости. Граф, который уже размещен на плоскости, называется плоским. Плоский и соответствующий ему планарный графы изоморфны. Условия плоской реализуемости графов определяет следующая теорема.

Теорема 2.2. (Понтрягина-Куратовского). Граф планарен, если ни один из его подграфов не гомеоморфен графам K ₅ и K _3,3.

На рис. 2.10 и 2.11 показаны планарные графы K ₅ и K _3,3, играющие важную роль в теории планарности и называемые графами Понтрягина-Кура­товского. Граф K ₅ – это полный граф с пятью вершинами. Он является предельным графом в том смысле, что если рассматривать последо­вательность полных графов, например, с семью, шестью, пятью и т.д. числом вершин, то граф K ₅ будет последним в этой последовательности непла­нар­ным графом с минимальным числом вершин. Полный граф с четырьмя вершинами является планарным. Кроме того, удаление хотя бы одного ребра из графа K ₅ делает его планарным.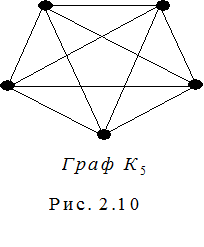

Двудольный граф K _3,3 также непланарен. Этот граф является моделью известной задачи о трех домах и трех колодцах: можно ли так проложить дорожки от всех домов к каждому колодцу, чтобы они не пересекались? Это соответствует ситуации. Когда поссорившиеся соседи не желают встре­чаться, но хотят пользоваться всеми колодцами.

Строгое доказательство теоремы Понтрягина-Куратовского приведено в[].

3. МАТРИЦЫ ГРАФОВ

Кроме рассмотренных в разделах 1 и 2 теоретико-множественной и геометрической форм определения (задания) графов, часто используется матричная форма их представления. Существуют различные виды матриц графов, однако все они, как правило, полностью передают основные свойства графов. Матричная форма задания графов обладает достаточной наглядностью при любой степени сложности графа и, что самое важное, позволяет автоматизировать процесс обработки информации, представленной в терминах теории графов, – любая матрица графа может быть введена в ЭВМ.

При задании графов в матричной форме могут учитываться либо отношения смежностей (вершин или ребер (дуг)), либо отображения инцидентности (вершин и ребер (дуг)). В связи с этим матрицы графов делятся на два основных класса: матрицы смежностей и матрицы инциденций.

Определение 3.1. Матрицей смежности вершин неориентированного графа G называется квадратная матрица A (G)=[ a_ij ] порядка p = p (G) (p – количество вершин графа), элементы a_ij которой равны числу ребер, соединяющих вершины x_i и x_j.

			x1	x2	x3	x4	x5	x6	x7	x8
		x1
		x2
		x3
A(G)	=	x4
		x5
		x6
		x7
		x8

На рис. 3.1 приведен неориентированный граф G (X, E) и справа – соответствующая ему матрица смежностей вершин A (G).

Из определения 3.1 непосредственно вытекают основные свойства матриц этого вида.

1. Матрица смежностей вершин неориентированного графа A (G) является квадратной и симметричной относительно главной диагонали.

2. Элементами матрицы A (G) являются целые положительные числа и число ноль.

3. Сумма элементов матрицы A (G) по i -й строке (или по i -му столбцу) равна степени соответствующей вершины d(x_i).

Из определения матрицы смежностей вершин неориентированного графа и ее основных свойств следуют некоторые особенности соответствия между графом G (X, E) и его матрицей A (G). На рис. 3.1 указана некоторая нумерация вершин графа; расположенная рядом матрица соответствует именно этой нумерации. Если же в графе G (X, E), приведенном на этом рисунке, использовать другую нумерацию вершин (например, сдвинув ее относительно вершин по часовой стрелке), то это приведет к тому, что в матрице A (G) произойдет перестановка отдельных строк и столбцов. Поэтому говорят, что каждый неориентированный граф имеет единственную с точностью до перестановки строк и столбцов матрицу смежностей вершин. И наоборот, каждая квадратная симметричная относительно главной диагонали матрица, элементами которой являются целые положительные числа и число ноль, определяет единственный с точностью до изоморфизма неориентированный граф, матрицей смежностей вершин которого является данная матрица.

Рекомендуется самостоятельно построить матрицу смежностей вершин графа G (X, E), показанного на рис. 3.1, с использованием другой нумерации вершин и сравнить полученную при этом матрицу с матрицей смежностей вершин приведенного графа.

Определение 3.2. Матрицей смежности вершин ориентированного графа G называется квадратная матрица A (G)=[ a_ij ] порядка n (n – число вершин графа), элементы которой a_ij равны числу дуг, исходящих из вершины x_i и заходящих в вершину x_j.

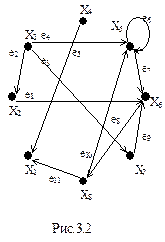
			x1	x2	x3	x4	x5	x6	x7	x8
		x1
		x2
		x3
A(G)	=	x4
		x5
		x6
		x7
		x8

На рис. 3.2 показан ориентированный граф G (X, E) и справа – матрица смежностей его вершин. Из определения следует, что сумма элементов i -й строки матрицы A (G) орграфа равна полустепени исхода d⁺(x_i), а по i -му столбцу – полустепени захода d^-(x_i). По-прежнему элементы этой матрицы – целые положительные числа и число ноль. Матрица смежностей вершин орграфа может оказаться симметричной относительно главной диагонали лишь в редких частных случаях.

Как и в случае неориентированных графов, каждый орграф имеет единственную с точностью до перестановки строк и столбцов матрицу смежностей вершин. И наоборот, каждая квадратная матрица, элементы которой – целые положительные числа и число ноль, определяет единственный с точностью до изоморфизма ориентированный граф.

Определение 3.3. Матрицей инцидентности неориентированного графа G называется матрица B (G)=[ b_ij ] размером (p x q) (p и q – количество вершин и ребер графа), элементы b_ij которой равны единице, если вершина x_i инцидентна ребру e_j и нулю, если соответствующие вершины и ребра не инцидентны.

Свойства матрицы инцидентности неориентированного графа.

1. Сумма элементов матрицы на i -й строке равна d(x_i).

2. Сумма элементов матрицы по i -му столбцы равна 2.

Матрица инцидентности графа, изображенного на рис. 3.1, а имеет вид:

e1

E2

e3

e4

e5

e6

e7

e8

e9

e10

x1

x2

x3

B(G)

=

x4

x5

x6

x7

x8

Следует отметить, что петле e_j =(x_i, x_i) в матрицах этого вида соответствует j -й столбец, состоящий из нулей и одной единицы, расположенной на i -м месте. Ребру e_k ={ x_m, x_n } соответствует в матрице инциденций k -й столбец, состоящий из нулей и двух единиц, расположенных на m -м и n -м местах. Нулевая строка матрицы соответствует изолированной вершине, а нулевой столбец – петле. Следует иметь ввиду, что нулевой столбец матрицы инцидентности лишь указывает на наличие петли, но не содержит информации о том, с какой именно вершиной связана эта петля.

Необходимо отметить, что между строками матрицы инцидентности B (G) существует очевидная зависимость. Так как каждый столбец этой матрицы содержит только два единичных элемента или состоит только из нулей, если столбец соответствует петле, то сумма по модулю 2 всех строк равна нулю. Поэтому без потери информации о графе вместо матрицы B (G) можно рассматривать сокращенную матрицу B _o(G), получаемую из B (G) вычеркиванием любой строки (чаще всего вычеркивается последняя строка). Таким образом, из p строк матрицы B (G) связного графа (см. п. 5) одна строка всегда линейно зависима, т.е. ранг матрицы B (G) не может превышать p -1 (ранг матрицы B (G) в точности равен p -1).

Любое подмножество столбцов матрицы B (G) можно рассматривать как матрицу инцидентности B´ (G) некоторого суграфа G ´(X, E ´), содержащего все вершины исходного графа и соответствующее выделенным столбцам подмножество E ´ CE его ребер. Все столбцы матрицы B´ (G) линейно независимы тогда и только тогда, когда суграф G ´(X, E ´) не содержит циклов. Действительно, если совокупность ребер образует цикл, то каждая вершина инцидента четному числу ребер этого цикла. Следовательно, сумма по модулю 2 соответствующих столбцов дает нулевой столбец, что означает из зависимость. Если же суграф не содержит циклов, то он имеет по меньшей мере две (вообще, четное число) концевых вершин, каждая из которых инцидентна только одному ребру, являющемуся концевым. Поэтому сумма по модулю 2 соответствующих столбцов будет содержать два (или четное число) единичных элемента и, следовательно, совокупность этих столбцов независима.

В связном графе с p вершинами всегда можно выделить p -1 ребер так, чтобы они образовали суграф без циклов, представляющий собой дерево графа, являющееся каркасом (см. п. 7). Поэтому матрица инцидентности содержит не менее p -1 независимых столбцов. В то же время любой суграф, имеющий более p -1 ребер, обязательно содержит цикл, т.е. в матрице инциденций не может быть больше p -1 независимых столбцов. Отсюда следует, что матрица инцидентности связного графа содержит в точности p -1 независимых столбцов, и поэтому ее ранг равен p -1. Число n= p -1 и определяет ранг графа.

Определение 3.4. Матрицей инцидентности орграфа G с p вершинами и q ребрами называется матрица B(G) = [b_ij] размером (p ´ q), элементы которой определяются следующим образом:

ì1, если вершина x_i является началом дуги e_j

b_ij = í -1, если вершина x_i является концом дуги e_{j ;}

_î 0, если вершина x_i не инцидентна дугу e_{j .}

Ниже приведена матрица инцидентности графа, изображенного на рис. 3.2:

e1

e2

e3

e4

e5

e6

e7

e8

e9

e10

e11

x1

-1

-1

x2

-1

x3

B(G)

=

x4

x5

-1

±1

-1

x6

-1

-1

-1

x7

-1

x8

-1

Матрица инцидентности орграфа G обладает следующими свойствами.

Сумма строк матрицы B(G) является нулевой строкой.

Любая строка матрицы B(G) является линейной комбинацией остальных строк.

Ранг матрицы B(G) равен p -1.

Определение 3.5. Матрицей смежности ребер неориентированного графа G называется квадратная матрица A^*(G) = [a^*_ij] порядка q, элементы a^*_ij которой равны единице, если ребра e_i и e_j

Дата добавления: 2014-01-06