Эйлеровы цепи и циклы

Рассматриваемая в этой главе задача является одной из самых ста­рей­ших в теории графов. В городе Кенигсберге (ныне Калининград) имелось семь мостов, соединяющих два берега реки Преголь, и два основа на ней друг с другом (рис. 7.1а). Требуется, начав путешествие из одной точки города прой­ти по всем мостам по одному разу и вернуться в исходную точку.

а) б)

Рис. 7.1.

Если поставить в соответствие мостам ребра, а участкам суши — вершины, то получится граф (точнее псевдограф), в котором надо найти про­стой цикл, проходящий через все ребра. В общем виде эта задача была решена Эйлером в 1736 г.

Дадим теперь

Определение 7.1. Эйлеровой цепью в неориентированном графе G назы­ва­ется простая цепь, содержащая все ребра графа G. Эйлеровым циклом назы­вается замкнутая Эйлерова цепь. Аналогично, эйлеров путь в орграфе G — это простой путь, содержащий все дуги графа G. Эйлеров контур в орграфе G — это замкнутый эйлеров путь. Граф, в котором существует эйлеров цикл, называется эйлеровым.

Простой критерий существования эйлерова цикла в связном графе дается следующей теоремой.

Теорема 7.1. (Эйлер) Эйлеров цикл в связном неориентированном графе G (X, E) существует только тогда, когда все его вершины имеют четную степень.

Доказательство. Необходимость. Пусть m - эйлеров цикл в связном гра­фе G, x — произвольная вершина этого графа. Через вершину x эйлеров цикл проходит некоторое количество k (k ³1) раз, причем каждое прохождение, очевидно, включает два ребра, и степень этой вершины равна 2 k, т.е. четна, так как x выбрана произвольно, то все вершины в графе G имеют четную сте­пень.

Достаточность. Воспользуемся индукцией по числу m ребер графа. Эйле­ровы циклы для обычных (не псевдо) графов можно построить начиная с m =3.Легко проверить, что единственный граф с m =3, имеющий все вершины с четными степенями, есть граф K ₃ (рис. 7.2). Существование эйлерова цикла в нем очевидно. Таким образом, для m =3 достаточность условий доказываемой теоремы имеет место. Пусть теперь граф G имеет m >3 ребер, и пусть утверждение справедливо для всех связных графов, имеющих меньше, чем m ребер. Зафиксируем произвольную вершину a графа G и будем искать простой цикл, идущий из a в a. Пусть m(a, x) — простая цепь, иду­щая из a в некоторую вершину x. Если x ¹ a, то цепь m можно продолжить из вершины x в некотором направлении. Через некоторое число таких про­дол­­же­ний мы придем в вершину z Î X, из которой нельзя продлить полу­чен­ную про­стую цепь. Легко видеть, что z = a так как из всех остальных вершин цепь может выйти (четные степени!); a в a она начиналась. Таким образом, нами построен цикл m, идущий из a в a. Предположим, что построенный про­стой цикл не содержит всех ребер графа G. Удалим ребра, входящие в цикл m, из графа G и рассмотрим полученный граф 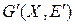. В графе 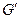все вершины имеют четные степени. Пусть — компо­нен­ты связ­нос­ти графа 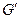, содержащие хотя бы по одному ребру. Соглас­но пред­поло­же­нию индукции все эти компоненты обладают эйлеровыми циклами m₁, m ₁, …, m _k соот­вет­ствен­но. Так как граф G связан, то цепь m встре­чает каждую из компонент. Пусть первые встречи цикла m с ком­понентами происходят соответственно в вершинах x ₁, x ₂, …, x_k. Тогда про­стая цепь

n(a, a)=m(a, x ₁) U m₁(x ₁, x ₁) U m(x ₁, x ₂) U…U m _k (x_k, x_k) U m(x_k, a)

является эйлеровым циклом в графе G. Теорема доказана.

Замечание. Очевидно, что приведенное доказательство будет верно и для псевдографов, содержащих петли и кратные ребра (см. рис. 7.1,а).

Таким образом, задача о кенигсбергских мостах не имеет ре­ше­ния, так как соответствующий граф (см. рис. 7.1,б) не имеет эйлерова цикла из-за не­четности степеней все вершин.

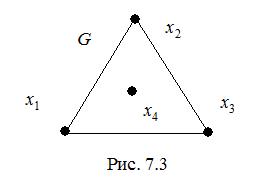Отметим, что из существования эйле­ро­ва цикла в неориентированном графе G не следует связность этого графа. Напри­мер, неориентированный граф G на рис. 7. 3 обладает эйлеровым циклом и вместе с тем несвязен.

Совершенно также, как теорема 7.1, могут быть доказаны следующие два утверждения.

Теорема 7.2. Связный неориентированный граф G обладает эйлеровой цепью тогда и только тогда, когда число вершин нечетной степени в нем равно 0 или 2, причем если это число равно нулю, то эйлерова цепь будет являться и циклом.

Теорема 7.3. Сильно связный орграф G (X, E) обладает эйлеровым кон­ту­ром тогда и только тогда, когда для любой вершины x Î X выполняется

.

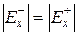Можно также обобщить задачу, которую решал Эйлер следующим обра­зом. Будем говорить что множество не пересекающихся по ребрам простых цепей 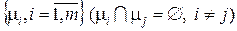графа G покрывает его, если все ребра графа G включены в цепи m _i. Нужно найти наименьшее количество таких цепей, которыми можно покрыть заданный граф G.

Если граф G — эйлеров, то очевидно, что это число равно 1. Пусть теперь G не является эйлеровым графом. Обозначим через k число его вер­шин нечетной степени. По теореме … k четно. Очевидно, что каждая верши­на нечетной степени должна быть концом хотя бы одной из покрывающих G цепей m _i. Следовательно, таких цепей будет не менее чем k /2. С другой сто­роны, таким количеством цепей граф G покрыть можно. Чтобы убедиться в этом, расширим G до нового графа , добавив k /2 ребер , соединяющих раз­личные пары вершин нечетной степени. Тогда оказывается эйлеровым графом и имеет эйлеров цикл 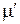. После удаления из 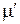ребер граф разло­жится на k /2 цепей, покрывающих G. Таким образом, доказана

Теорема 7.4. Пусть G — связный граф с k >0 вершинами нечетной степени. Тогда минимальное число непересекающихся по ребрам простых цепей, покрывающих G, равно k /2.

Дата добавления: 2014-01-06