Обоснование алгоритма. Предположим, что уже построена простая цепь mk-1 = {e1, e2, , ek-1} для k³2 методом, указанным в алгоритме

Предположим, что уже построена простая цепь m _{k -1} = { e ₁, e ₂, …, e_{k -1}} для k ³2 методом, указанным в алгоритме. Пусть e_{k -1} = (x_{k -2}, x_{k -1}) и x_{k -1} ¹ a. Рас­смо­трим подграф , который получается из подграфа G_{k -1}(X, E\ m _{k -1}) удалением всех изолированных вершин. Вершина x_{k -1} в этом подграфе имеет нечет­ную степень, поэтому существует по крайней мере одно ребро e_k Î E\ m _{k -1}, ин­ци­дентное x_{k -1}. Если это ребро единственное, то оно не является мостом в графе . В противном случае вершина a будет связана с некоторой вер­ши­ной единственной цепью, содержащей ребро e_k, что противоречит суще­ствованию эйлерова цикла в графе G. Поскольку e_k - не мост, то процесс мож­но продолжать, взяв . Если ребро e_k не единственное инци­дентное вершине x_{k -1}, то среди этих ребер есть по крайней мере одно, не явля­ющееся мостом. В противном случае один из этих мостов можно выбро­сить так, что вершины x_{k -1} и a попадут в разные компоненты связности графа . Если x_{k -1} принадлежит компоненте M, то в этой компоненте все вер­шины имеют четную степень, поэтому существует эйлеров цикл в M, про­хо­дящий через x_{k -1}. Этот цикл содержит все ребра, инцидентные x_{k -1} и при­над­лежащие , являющиеся одновременно мостами. Получено противоречие, так как ребра из эйлерова цикла мостами быть не могут. Итак, в рассмотренном случае существует ребро e_k, инцидентное вершине x_{k -1} и не являющееся мостом. Значит, и в этом случае процесс можно продолжать, взяв

.

Из предыдущего следует, что процесс нельзя продолжать тогда и только тогда, когда мы попадем в вершину a, причем степень вершины a относительно непройденных ребер равна нулю. Докажем, что в этом случае построенный цикл m - простой цикл. Покажем, что m содержит все ребра графа G. Если не все ребра графа G принадлежат m, то не принадлежащие m ребра порождают компоненты связности C ₁, …, C_m (m ³1) в подграфе . Пусть компонента C_i, 1£ i £ m соединяется с циклом m в вершине y_i. Если существует ребро e Îm, такое, что e =(y_i, a), то при построении цикла m было нарушено правило выбора ребра e, что невозможно. Если часть цикла m, соединяющая y_i и a, состоит более чем из одного ребра, то первое ребро этой части 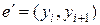было мостом, и поэтому было нарушено правило вы­бора , что невозможно. Итак, непройденных ребер быть не может, поэ­тому m - эйлеров цикл.

8.НАХОЖДЕНИЕ КРАТЧАЙШИХ ПУТЕЙ В ГРАФЕ

В этом параграфе рассматриваются ориентированные графы G (X, E) каждой дуге e Î E которого ставится в соответствие вещественное число l (e). Т.е. на множестве Е создана функция l: E ® R. Такой граф принято называть нагруженным. Само число l называется весом дуги.

Можно увидеть аналогию между, например, картой автомобильных или железных дорог. Тогда множество вершин Х будет соответствовать городам, множество дуг – магистралям, соединяющим города, а веса – расстояниям. (На практике, при этом, фактически получится неориентированный граф).

В связи с изложенной аналогией будем называть веса дуг расстояниями.

Определение 8.1. Пусть имеется последовательность вершин x ₀, x ₁, …, x_n, которая определяет путь в нагруженном графе G (X, E), тогда длина этого пути определяется как .

Естественный интерес представляет нахождение кратчайшего пути между двумя заданными вершинами x и y.

Алгоритм Форда отыскания кратчайшего пути.

Будем предполагать, что все расстояния в графе положительны. (Если это не так, то ко всем весам можно всегда добавить такую константу, что все эти веса станут положительными).

Пусть мы ищем путь от вершины x ₀ к вершине x_n. Будем каждой вершине x_i ставить в соответствие некоторое число l _i по следующим правилам.

1° Положим l₀= 0, l _i = ¥ (достаточно большое число) для " i > 0.

2° Ищем в графе дугу (x_i, x_j) удовлетворяющую следующему условию

l _j - l _i > l (x_i, x_j), (1)

после чего заменяем l _j на

.

Пункт 2° повторяется до тех пор, пока невозможно будет найти дугу, удовлетворяющую условию (1). Обоснуем этот алгоритм и укажем как определяется кратчайший путь.

Отметим, что l _n монотонно уменьшается, то после завершения алгоритма найдется дуга , такая, что для которой последний раз уменьшалось l _n. (Иначе вообще нет пути между x ₀ и x_n или для верно (1)).

По этой же самой причине найдется вершина , такая, что

,

этот процесс может продолжаться и дальше, так что получится строго убыва­ю­щая последовательность . Отсюда следует, что при некото­ром k мы получим .

Покажем, что – минимальный путь с длиной l _n, т.е. длина любого другого пути между x ₀ и x_n не превышает k_n.

Возьмем произвольный путь и рассмотрим его длину .

После завершения алгоритма имеем следующие соотношения

Сложив все эти неравенства, получим

,

что и требовалось доказать.

Рассмотрим пример.

а б

Рис. 8.1

На рис. 1а изображен исходный помеченный граф и начальные значения l _i. На рис. 1б для того же графа указаны конечные значения l _i и выделен кратчайший путь. Пометка вершин графа происходила в следующем порядке (в скобках указана дуга, вдоль которой выполняется (1)):

l₁ = 6 (x ₀, x ₁),

l₂ = 7 (x ₀, x ₂),

l₃ = 6 (x ₀, x ₃),

l₄ = 12 (x ₁, x ₃),

l₄ = 11 (x ₂, x ₄),

l₅ = 16 (x ₃, x ₄),

l₅ = 15 (x ₄, x ₅),

l₆ = 18 (x ₄, x ₆),

l₆ = 17 (x ₅, x ₆).

Иногда возникает задача отыскания кратчайших расстояний между всеми парами вершин. Одним из способов решения этой задачи является

Дата добавления: 2014-01-06