Синтаксическая мера информации. Для измерения информации вводятся два параметра: количество информации I и объем дан­ных VД

МЕРЫ ИНФОРМАЦИИ

Классификация мер

Для измерения информации вводятся два параметра: количество информации I и объем дан­ных V_Д.

Эти параметры имеют разные выражения и интерпретацию в зависимости от рассмат­риваемой формы адекватности. Каждой форме адекватности соответствует своя мера коли­чества информации и объема данных (рис. 2.1).

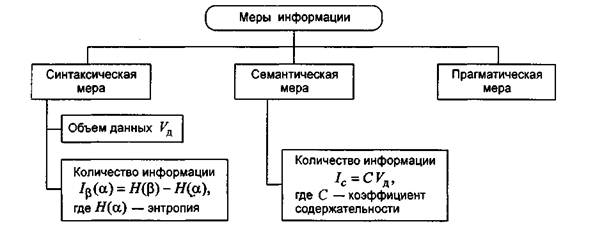
Рис. 2.1. Меры информации

Эта мера количества информации оперирует с обезличенной информацией, не выражающей смыслового отношения к объекту.

Объем данных V_Д в сообщении измеряется количеством символов (разрядов) в этом сообщении. В различных системах счисления один разряд имеет различный вес и соот­ветственно меняется единица измерения данных:

в двоичной системе счисления единица измерения — бит (bit — binary digit — двоич­ный разряд);

Примечание. В современных ЭВМ наряду с минимальной единицей измерения данных "бит" широко используется укрупненная единица измерения "байт", равная 8 бит.

в десятичной системе счисления единица измерения — дат (десятичный разряд).

Пример 2.3. Сообщение в двоичной системе в виде восьмиразрядного двоичного кода 10111011 имеет объем данных V_Д = 8 бит.

Сообщение в десятичной системе в виде шестиразрядного числа 275903 имеет объем данных V_Д = 6 дит.

Количество информации I на синтаксическом уровне невозможно опреде­лить без рассмотрения понятия неопределенности состояния системы (энтропии системы). Действительно, получение информации о какой-либо системе всегда связано с изменением степени неосведомленности получателя о состоянии этой системы. Рассмотрим это понятие.

Пусть до получения информации потребитель имеет некоторые предварительные (ап­риорные) сведения о системе α. Мерой его неосведомленности о системе является функция H(α), которая в то же время служит и мерой неопределенности состояния системы.

После получения некоторого сообщения β получатель приобрел некоторую дополни­тельную информацию Iβ(α), уменьшившую его априорную неосведомленность так, что апостериорная (после получения сообщения β) неопределенность состояния системы стала Hβ(α).

Тогда количество информации Iβ(α) о системе, полученной в сообщении β, опреде­лится как

Iβ(α) = H(α) - Hβ(α),

т.е. количество информации измеряется изменением (уменьшением) неопределенности со­стояния системы.

Если конечная неопределенность Hβ(α) обратится в нуль, то первоначальное непол­ное знание заменится полным знанием и количество информации Iβ(α) = H(α). Иными сло­вами, энтропия системы H(α) может рассматриваться как мера недостающей информации.

Энтропия системы H(α), имеющая N возможных состояний, согласно формуле Шенно­на, равна:

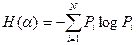
где p_i — вероятность того, что система находится в i-м состоянии.

Дня случая, когда все состояния системы равновероятны, т.е. их вероятности равны Pi =, ее энтропия определяется соотношением

Часто информация кодируется числовыми кодами в той или иной системе счисления, особенно это актуально при представлении информации в компьютере. Естественно, что одно и то же количество разрядов в разных системах счисления может передать разное число состояний отображаемого объекта, что можно представить в виде соотношения

N=mⁿ,

где N — число всевозможных отображаемых состояний;

т — основание системы счисления (разнообразие символов, применяемых в алфавите); п — число разрядов (символов) в сообщении.

Пример 2.4. По каналу связи передается n-разрядное сообщение, использующее т различных символов. Так как количество всевозможных кодовых комбинаций будет N=mⁿ, то при равновероятности появления любой из них количество информации, приобретенной абонентом в результате получения сообщения, будет I = log N = п log т — формула Хартли.

Если в качестве основания логарифма принять т, то I = п. В данном случае количест­во информации (при условии полного априорного незнания абонентом содержания сообщения) будет равно объему данных I = V_Д, полученных по каналу связи. Для неравновероятных состояний системы всегда I < V_Д = n.

Наиболее часто используются двоичные и десятичные логарифмы. Единицами измере­ния в этих случаях будут соответственно бит и дит.

Коэффициент (степень) информативности (лаконичность) сообще­ния определяется отношением количества информации к объему данных, т.е.

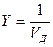, причем 0<Y<1.

С увеличением Y уменьшаются объемы работы по преобразованию информации (дан­ных) в системе. Поэтому стремятся к повышению информативности, для чего разрабатыва­ются специальные методы оптимального кодирования информации.

Дата добавления: 2014-01-06