
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Примеры. Основы защиты информации
|
|
|
|
Основы защиты информации
2.1. Цели защиты информации.
2.2. Направления защиты информации.
2.3. Понятие системы безопасности информации.
2.4. Правовые методы защиты информации: авторское право (понятие автора, имущественные и неимущественные права), патентная защита (понятие), государственная тайна и производственные секреты (понятия), лицензионные соглашения и контракты (понятие лицензии, типы лицензий, типы программ по юридическому статусу).
2.5. Программные методы защиты информации: защита от несанкционированного доступа (понятия и назначение парольной защиты, электронных ключей, брендмауэров, криптографических методов), защита от компьютерных вирусов (понятие компьютерного вируса, признаки «заражения»).
|
Текст на русском языке – избыточность 20-25%.
Визуальная информация – избыточность 90%.
Чем выше избыточность, тем больше методов её восприятия.
С помощью избыточности информации повышают её достоверность с помощью спец. вар. И статистических методов.
5) Объективность и субъективность информации – относительные понятия. Так как сами методы являются субъективными. Более объективно рассматривать фотоснимок объекта, а не его рисунок.
6) Доступность информации определяется доступностью как данных. Так и методов её воспроизведения
7) Актуальность информации – степень соответствия информации текущему моменту времени.
Единица количества информации
Два подхода.
Первый. Вероятностный. Получатель данных или сообщений имеет определённое представление о возможности наступления некоторых событий. Эти представления в общем случае недостоверны и выражены вероятностями, с которыми он ожидает то или иное событие. Общая мера неопределённости (энтропия). Характеризуется некоторой тематической зависимостью совокупности этих вероятностей.
Н – энтропия некоторого события.
m – количество возможных исходов события.
Для оценки информации используется формула Хартли: 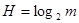 .
.
В случае колоды из тридцати двух карт данная формула даёт число двоичных вопросов, ответами на которые могут быть «да» и «нет».
Дама Пик
1) Масть красная - 0
2) Трефы – 0
3) Одна из четырёх старших – 0
4) Одна из двух старших - 0
5) Дама – 1
В общем случае энтропия зависит не только от числа возможных исходов. Но и от вероятности их исходов.
Шенноном предложена формула 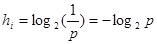 .
.
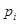 – вероятность наступления i-го исхода.
– вероятность наступления i-го исхода.
Тогда энтропия, приходящаяся на некоторый алфавит из n символов 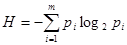 .
.
Можно статистически определить частоту употребления буквы.
Для русского языка информативность 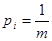
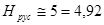
Для английского алфавита 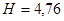 .
.
Частотность символов в русском языке
1) Пробел – 0,175
2) о – 0,09
3) е – 0,072
4) ё – 0,072
5) а – 0,062
6) и – 0,062
12) л – 0,035
21) ь – 0,014
22) ъ – 0,014
33) э – 0,003
34) ф – 0,002
printer = prn
Количественный подход к определению количества информации
Важным при определении количества информации является определение единицы информации.
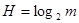

Единицей информации называют бит (binary digit), что в двоичном коде эквивалентно нулю и единицей.
Выбор нуля и единицы не случаен, так как:
1) наиболее просто реализуется аппаратно;
2) позволяет на одной и той же аппаратуре производить как арифметические. Так и логические операции.
Другая не случайно выбранная единица информации – байт, равная восьми битам. 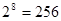
Таким образом, восьми бит достаточно для кодирования двух национальных алфавитов, строчных и прописных, различных специальных символов.
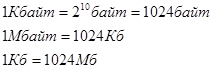
Системы счисления в ЭВМ
В ЭВМ используются позиционные системы счисления: двоичная, восьмеричная шестнадцатеричная и десятичная.
В позиционной системе счисления каждая цифра 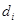 имеет свой весовой коэффициент
имеет свой весовой коэффициент 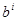 , где b – основание системы счисления, i – номер позиции цифры в числе. Общая форма записи чисел в таких системах:
, где b – основание системы счисления, i – номер позиции цифры в числе. Общая форма записи чисел в таких системах: 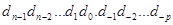 . А значение рассчитывается по формуле:
. А значение рассчитывается по формуле: 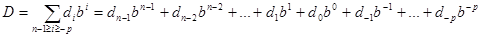 .
.
Пример. 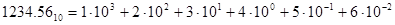 .
.
В ЭВМ используется двоичная система счисления, основание которой равняется 2, и каждая цифра может принимать два значения: 0 и 1.
Два способа такой записи:
1) Арифметический (вначале записывается кодовая комбинация из одних нулей 0000, затем каждой предыдущей строке добавляется единица с организацией переноса в старшие разряды).
2) Формальный (вначале записывается столбец младшего разряда, в котором на каждой строке происходит смена нулей и единиц, в каждом последующем столбце частота смены единиц и нулей уменьшается вдвое).
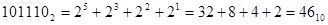
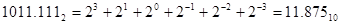
Кроме двоичной в ЭВМ используется восьмеричная система счисления с основанием 8 (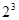 ) и шестнадцатеричная с основанием 16 (
) и шестнадцатеричная с основанием 16 (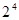 ).
).
Восьмеричная использует цифры: 0, 1, 2, 3, 4, 5, 6, 7.
Шестнадцатеричная использует цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
0 000 0 0000 0
1 001 1 0001 1
2 010 2 0010 2
3 011 3 0011 3
4 100 4 0100 4
5 101 5 0101 5
6 110 6 0110 6
7 111 7 0111 7
8 1000 8
9 1001 9
10 1010 A
11 1011 B
12 1100 C
13 1101 D
14 1110 E
15 1111 F
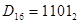
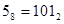
Чтобы перевести целое двоичное число в восьмеричное (шестнадцатеричное), необходимо, двигаясь влево от десятичной точки, делить его на группы по 3 (4) бита. Затем каждая группа заменяется на одну восьмеричную (шестнадцатеричную) цифру.
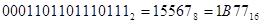
При необходимости к последней группе приписываются нули.
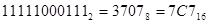
Дробные числа переводятся аналогично, но деление на группы проводится, двигаясь вправо от десятичной точки и записывая недостающие нули, являющиеся значащими.
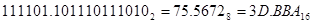

Для преобразования восьмеричных и шестнадцатеричных чисел в двоичные, необходимо каждую восьмеричную цифру заменить тремя двоичными, шестнадцатеричную – четырьмя.
Преобразование из восьмеричной в шестнадцатеричную возможно с помощью предварительного перевода в двоичную.
Перепишем общую формулу расчёта в позиционной системе счисления в следующем виде
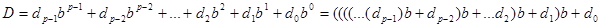 .
.
Если данную формулу разделить на основание системы счисления b, в остатке получим 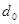 , а частное примет вид общей формулы, но на одно слагаемое меньше.
, а частное примет вид общей формулы, но на одно слагаемое меньше.
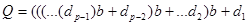
Если Q разделить на основание системы счисления, то получим вторую цифру.
Общая формула.
Если число в системе C необходимо перевести в систему S, то для этого нужно провести его последовательное деление на основание системы S, выраженное в системе C. На каждом шаге деления получают цифры числа в системе S, начиная с младшей. Процесс деления заканчивается, когда частное станет меньше S.
Схема Горнера
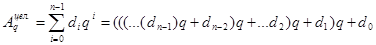 .
.
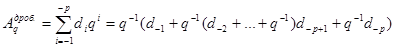 .
.
Отдельно для целой и дробной части числа в произвольной системе счисления.
Пример. 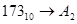
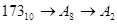
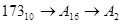


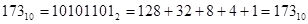 .
.
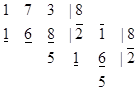
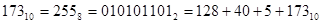 .
.
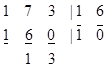
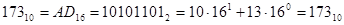 .
.
При вводе в ЭВМ каждая десятичная цифра заменяется четырьмя двоичными битами. Такая запись десятичных чисел называется двоично-десятичной.
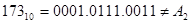 - это не двоичный код.
- это не двоичный код.
Двоичное значение двоично-десятичного числа осуществляется по схеме Горнера.
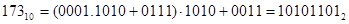
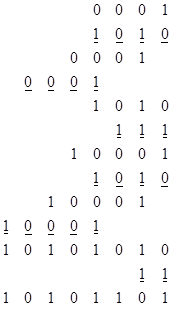
Аналогично по схеме Горнера можно получить правила перевода дробных чисел из одной системы счисления в другую, но так как там основание системы счисления в отрицательной степени, перевод сводится к ряду последовательных умножений.
Правило1: последовательно умножать переводимое число и полученные дробные части на основание новой системы, выраженное в алфавите исходной, до тех пор, пока дробная часть не станет равной нулю или пока не будет достигнута заданная точность.
Правило2: полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, выразить в алфавите этой системы.
Правило3: записать дробную часть числа в новой системе, начиная с целой части первого произведения.
Пример. 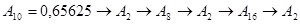 .
.
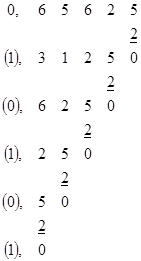
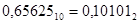 .
.
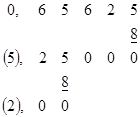
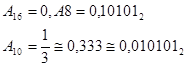
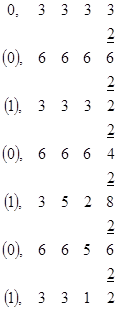
В частном случае, если знаменатель дробной части представляет целую степень числа, то числитель a переводится как целое b k двоичных бит.
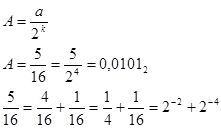
Смешанные числа переводятся по отдельности: целая часть и дробная часть.
Три способа перевода чисел из одной системы счисления в другую:
1) По правилам (триады, тетрады).
2) По степенному ряду.
3) По схеме Горнера.
Пример. 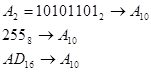
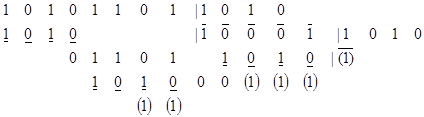
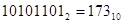 .
.


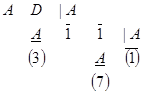
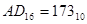
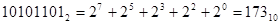
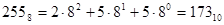
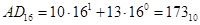
Двоичная арифметика
Сложение
0+0=0
0+1=1
1+0=1
1+1=0 выходной перенос = 1
| x | y | 
| 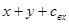
| 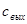
|
10110110=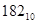
+1101110=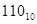
+101101=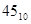
+10111=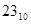
--------------------
101101000=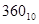
Вычитание
0-0=0
0-1=1 выходной перенос = 1
1-0=1
1-1=0
| x | y | 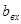
| 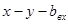
| 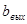
|
Пример. 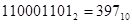
-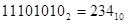
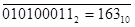
В ЭВМ вычитание проводится в виде А-В=А+(-В). Для того отрицаемое слагаемое представляется в дополнительном коде или в коде с дополнением до двух. Чтобы получить дополнительный код двоичного число необходимо проинвертировать его прямой код и к результату прибавить единицу.
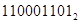
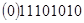
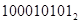
+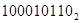 +
+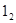
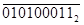
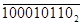
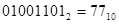
-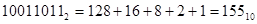
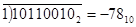
При вычитании с помощью прямого кода признаком отрицательного результата является наличие окончательного заёма за пределы разрядной сетки. В этом случае результат получаем в дополнительном коде и для определения его абсолютной величины необходимо перейти к прямому.
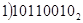
-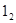
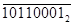
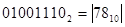
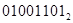
+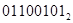
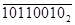
При вычитании с помощью дополнительного кода признаком положительного результата является наличие окончательного переноса за пределы разрядной сетки.
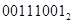

+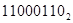 +
+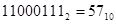
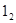
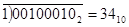
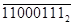
1) – это не цифра, это знак результата.
Для указания знака числа отводится специальный старший двоичный разряд (или бит). У положительного числа он равен нулю, у отрицательного – единице.
С помощью байта, в котором старший 7-разряд отведён под знак числа, можно представлять числа от –127 до 127.
При сложении двух чисел, в сумме превышающим 127 происходит искажение результата за переполнения разрядной сетки.

+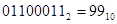
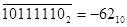
Переполнение произошло, если слагаемые имеют одинаковые знаки, а сумма или противоположна.
Умножение
В начале множимое умножается на младший разряд множителя, получаем первое частичное произведение, затем на второй разряд множителя, получаем второе частичное произведение, но сдвинутое относительно первого на один разряд влево и так далее. Полное произведение получаем суммированием всех частичных.

*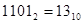

+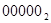
+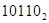
+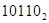
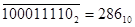
22*13=286
Деление
Деление – это последовательное вычитание делителя из делимого, начиная со старших разрядов со сдвигом делителя вправо на один разряд на каждом шаге. На каждом шаге анализируем знак остатка, если он отрицательный, остаток игнорируется, в частное записывается ноль, из делимого снимается следующая цифра, делитель сдвигается на одну позицию вправо.
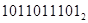 |
|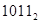
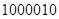
-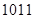
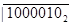 *
*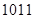
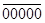
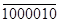
-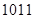 +
+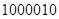
 +
+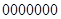
-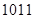 +
+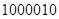
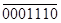

-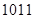 +
+
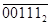
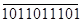
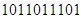 |
|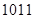 1011
1011
+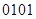
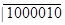 0100
0100
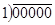 +1
+1
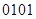
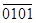

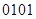
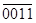
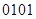
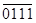
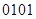
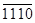
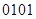

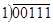

Формы и форматы представления
числовых данных в ЭВМ
В ЭВМ каждый двоичный бит реализуется с помощью бистабильного элемента триггера, одно из составляющих которого соответствует нулю, другое – единицы.
Совокупность определённого числа таких элементов служит для представления многоразрядных двоичных чисел и представляет собой разрядную сетку или формат представления числовых данных.
В ЭВМ используется как естественная, так и нормальная форма предсавления чисел. Каждая форма имеет свои форматы, состоящие из целого числа байт.
ЕС ЭВМ – единая серия ЭВМ.
ЕС ЭВМ: полуслово – 2 байт, слово – 4 байта, двойное слово – 8 байт.
ПЭВМ: слово – 2 байта.
Естественная форма:
Естественная форма предназначена для хранения чисел с фиксированной точкой. Для правильных дробей – перед старшим разрядом, для целых чисел – после младшего разряда.
Во всех форматах знак числа занимает место перед старшим разрядом (0 ® +, 1 ® -).
Два формата:
| Н | … | 2 байта | ||||||
| … | ||||||||
| … |

| F | … | ||||||
| … | |||||||
| … |
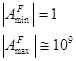
Для сокращения записи можно использовать шестнадцатеричную систему.
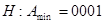
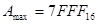
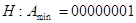

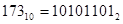
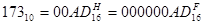
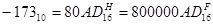
По первой цифре можно определить знак числа. Если оно меньше 8, то число положительное, если больше 8 – отрицательное.
Достоинства форматов: простота и наглядность.
Недостатки: ограниченный диапазон представляемых чисел, возможность переполнения разрядной сетки.
Нормальная форма:
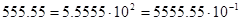
В нормальной форме числа представляются как 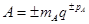 , где
, где 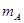 – мантисса числа, p – его порядок, q – основание системы счисления.
– мантисса числа, p – его порядок, q – основание системы счисления.
Для однозначности представления чисел мантисса должна удовлетворять условиям:
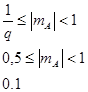
Для представления нормальных чисел используются стандартные форматы разной длины. Старший разряд (31) отводится под знак числа, 30 бит отводится под знак порядка, 24-29 – порядок числа, 0-23 – мантисса числа.
| Знак числа | Знак порядка | Порядок числа (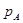 ) )
| Мантисса числа (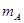 ) )
| ||||||||
| … |

Особенности нормальной формы: смещение числовой оси порядков в область положительных значений для облегчения действий над порядками. Не имеющими знака. В формате под порядок отводится 6 бит и седьмой под его знак, следовательно числовая ось лежит в диапазоне
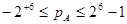
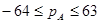
Смещ. порядок, назыв. характеристикой, опред. смещ. порядка вправо на 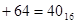 . Если характеристика равн.
. Если характеристика равн. 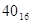 , то порядок равен нулю, если меньше – порядок отрицательный, если больше – порядок положительный. Если характеристика меньше нуля или больше
, то порядок равен нулю, если меньше – порядок отрицательный, если больше – порядок положительный. Если характеристика меньше нуля или больше 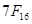 , произошло переполнение порядка и искажение результатов.
, произошло переполнение порядка и искажение результатов.
Мантиссы и порядки выраж. в шестнадцатеричной системе счисления в двоичном коде, что позволяет увеличить диапазон представл. чисел в 4 раза.
Пример. 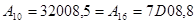
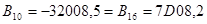
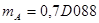
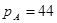
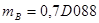
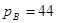
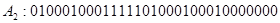
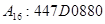
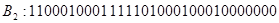
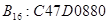
Машинные коды
В ЭВМ все арифметические операции сводятся к сложению и сдвигу чисел влево или вправо. При этом учитываются знаки чисел, опред. знак результата и факт наличия и отсутствия переполнения разрядной сетки.
Замена вычитания на сложение может проводиться с помощью дополнительного и обратного кода. Их суть состоит в том, что отрицательное слагаемое представл. в виде дополнения до некоторой константы K, такой, что K-B>0. Обратный и дополнительный коды отличаются выбором этой константы.
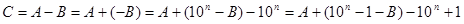 , где 10 – основание системы счисления,
, где 10 – основание системы счисления,  – const при введении дополнительного, (
– const при введении дополнительного, ( -1) – const обратного кода, n – количество разрядов представл. целых чисел в данной системе счисления.
-1) – const обратного кода, n – количество разрядов представл. целых чисел в данной системе счисления.
Из полученной суммы необходимо изъять добавленную константу.
Пример. 59|2 1 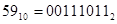
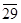 |2 1
|2 1
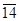 |2 0
|2 0
 |2 1
|2 1
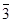 |2 1
|2 1
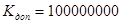
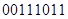
-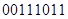 +
+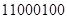
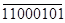 +1
+1
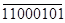
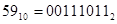 Пк
Пк
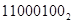 Дк
Дк
С=59-34
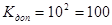
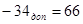
+66
 -100=25
-100=25
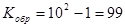
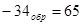
+65
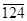 -100=24
-100=24
+1
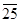
В случае дополнительного кода его константа компенсируется ликвидацией ед. переноса из старшего разряда. А в случае обратного кода – ликвидацией единицы и прибавления её к результату, то есть на одну операцию больше. Поэтому для реального вычитания используется дополнительный код, а обратный используется для получения дополнительного.
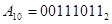

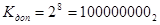
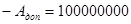
-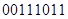
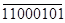
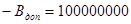
-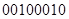

С=А-В
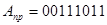
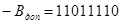
+11011110
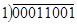
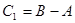
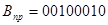
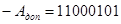
+11000101

-11100111
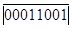 – модуль результата
– модуль результата
При сложении чисел с разными знаками единица переноса из старшего разряда является признаком положительного результата, отсутствие переноса – признаком отрицательного результата. При этом код результата находится в дополнительном коде. Чтобы получить его модуль, необходимо скомпенсировать константу дополнительного кода.
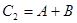
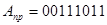
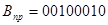
+00100010
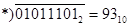 *) – отсутствует
*) – отсутствует
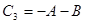
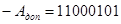
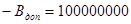
11000101 100000000
+11011110 -10100011
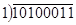
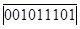
При сложении чисел с одинаковыми знаками признаки противоположны. При сложении положительных чисел признаком положительного результата является отсутствие переноса из старшего разряда, признаком отрицательного результата – его наличие. Эти же признаки говорят об отсутствии переполнения разрядной сетки.
200|2 0
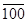 |2 0
|2 0
 |2 0
|2 0
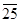 |2 1
|2 1
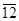 |2 0
|2 0
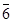 |2 0
|2 0
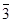 |2 1
|2 1
 1
1
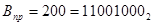
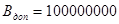
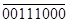
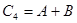
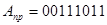
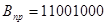
+11001000
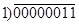
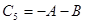
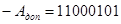
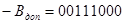
11000101 100000000
+00111000 -11111101
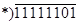
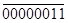
Правила построения дополнительного и обратного кода на примере чисел 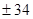 . Старший бит отведён под знак числа.
. Старший бит отведён под знак числа.
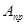
| 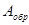
| 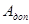
| |
| +34 | |||
| -34 | 1.0100010 |
-00100010
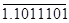
|
-00100010
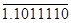
|
1) Прямой код положительного и отрицательного числа отличаются только знаковыми разрядами.
2) Прямой, дополнительный и обратный коды положительных чисел совпадают.
3) Обратный код отрицательного числа образуется из прямого кода положительного числа путём инверсии кода, включая знаковый разряд.
4) Дополнительный код отрицательного числа образуется дополнением единицы к младшему разряду обратного кода или путём инверсии прямого кода, исключая последнюю единицу и следующие за ней нули.
Числа в естественной форме хранятся в ЭВМ в дополнительном коде, в нормальной форме – в прямом коде.
Действия над числами, представленными в естественной форме
1) Числа в естественной форме в памяти хранятся в дополнительном коде.
2) В сумматоре числа складываются вместе со знаками, при этом образуется знак результата.
3) При сложении чисел с разными знаками единица переноса из знакового разряда стирается, то есть компенсируется константа дополнительного кода.
4) При сложении чисел с одинаковыми знаками признаками переполнения разрядной сетки являются:
- знак суммы не соответствует знакам слагаемых;
- переносы из старшего разряда суммы в знаковый и из знакового за пределы разрядной сетки не согласуются.
Пример. 
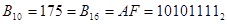
Работаем в двух байтах. Составляем коды.

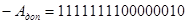
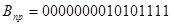

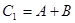

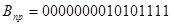
 >0
>0
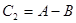


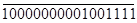 >0
>0
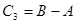
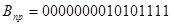
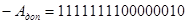
 – дополнительный код
– дополнительный код
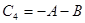
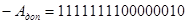

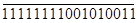
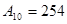
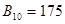
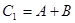
1) При получении сумм двух чисел с одинаковыми знаками переполнение разрядной сетки не произошло, так как знак суммы совпадает со знаками слагаемых и переносы из старшего разряда в знаковый и из знакового согласуются.
2) При получении сумм 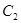 и
и 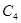 образуется перенос из знакового разряда, который необходимо исключать..
образуется перенос из знакового разряда, который необходимо исключать..
3) Суммы 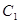 ,
, 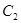 – положительные,
– положительные, 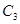 ,
, 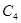 – отрицательные.
– отрицательные. 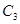 ,
, 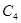 хранятся в памяти в дополнительном коде, то есть без преобразования.
хранятся в памяти в дополнительном коде, то есть без преобразования.
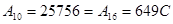
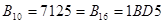
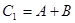
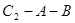
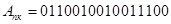
+
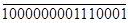
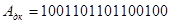
+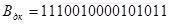
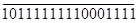
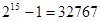
В обоих примерах произошло переполнение разрядной сетки за допустимые пределы: знаки сумм не соответствуют знакам слагаемых и переносы из старшего разряда в знаковый и из знакового разряда не согласуются.
Действия над числами, представленными в нормальной форме
1) Числа в нормальной форме хранятся в памяти в прямом коде с нормализованными мантиссами.
2) Сложение чисел проводится путём сложения их мантисс при одинаковых характеристиках слагаемых. За общий выбирается наибольший порядок. Выравнивание порядков слагаемых проводится путём сдвига вправо мантиссы меньшего числа.

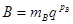
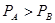

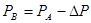

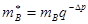
3) При сложении мантисс с одинаковыми знаками возможно переполнение разрядной сетки, что будет являться нарушением нормализации влево. Для его устранения необходим сдвиг мантиссы на один разряд вправо и соответ. увелич. характ. на 1.
4) Результаты в прямом коде нормализуются.
5) Действия в сумматоре выполняются над кодами мантисс, которые поступают из регистров в младшие 24 бита сумматора, знаки мантисс и характеристики заносятся в специальные схемы, которые обеспечивают выравнивание характ., норм. мантиссы рез., формирование знака результата и характеристики результата. Старшие разряды сумматора 24-31 заполняются нулями.
6) Алгоритмы сложения после выравнивания характеристик зависят от знаков слагаемых:
- если знаки одинаковые, модули мантисс (прямые коды) суммируются. Переполнение определяется наличием переноса единицы из старшего разряда мантиссы в 24 бит, что вызывает нарушение нормализации мантиссы влево. Нормализация проводится сдвигом на одну шестнадцатую вправо. Старшая тетрада мантиссы заполняется кодом 0001. Характеристика результата увеличивается на 1. В регистре результата сумматора форм. рез. операции:
схема анализа знака и характеристик
В 31-й заносят знак результата. В 30-24 – характеристика. 23-0 – мантисса в прямом коде;
- если знаки слагаемых различны, отрицательная мантисса преобразуется в дополнительный код и мантиссы суммируются. Признаком положительного результата является перенос из старшего разряда мантиссы в младший характеристики, кот. стирается. Признаком отрицательного результата – его отсутствие. При этом мантисса представляется в дополнительном коде и должна быть преобразована в прямой. При сложении чисел с разными знаками возможно нарушение нормализации мантиссы вправо, тогда старшая 16-ая цифра мантиссы равна нулю. Нормализацию проводят сдвигом на 16-ую цифру влево и уменьшением характеристики на 1. После этого в регистре форм. результат. Знаковый разряд заносят в знаковый разряд большего по модулю слагаемого.
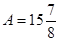 ;
; 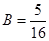 ;
;
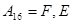 ;
; 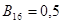 ;
;
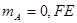 ;
; 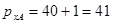 ;
;
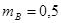 ;
; 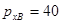 ;
;
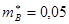 ;
;
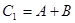 ;
;
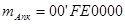 ;
; 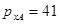 ;
;
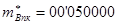 ;
; 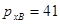 ;
;
 ;
; 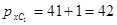 ;
;
Единица переноса из старшего разряда в характеристику характеризует переполнение разрядной сетки. Это нарушение нормализации влево. Мантиссу необходимо сдвинуть на одну 16-ую вправо, порядок увеличить на 1.
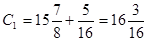
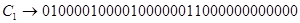
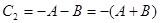
Мантисса складывается в прямых кодах, в знаковый разряд результата записывается знак одного из слагаемых.
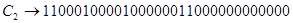
С2103000
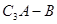 ;
; 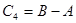
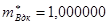
-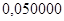
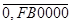
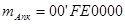
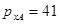
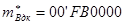
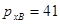
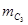
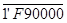
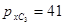
Так как слагаемые имеют разные знаки, то единица переноса из старшего разряда мантиссы является признаком положительного результата и должна быть стёрта для компенсации константы дополнительного кода.
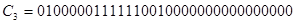

-
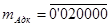
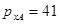
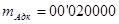
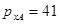
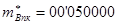
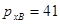

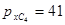
Переноса из старшего разряда мантиссы нет, поэтому результат отрицательный находится в дополнительном коде и должен быть переведён в прямой.
-0070000


С1F90000
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 416; Нарушение авторских прав?; Мы поможем в написании вашей работы!