Построение графиков функций. Подготовка диаграммы к печати

Подготовка диаграммы к печати

Изменение размера области диаграммы

Форматирование легенды

Вставка названий

Для этого необходимо вызвать контекстно-зависимое меню форматирования области диаграммы или пункт основного меню Excel Вставка и выбрать Вставить названня=Присоединить текст. Здесь название можно ввести двумя способами: непосредственно ввести в текстовое поле или сослаться на ячейку, содержащую его.
1. Выберем в меню Вставить названия, присоединить текст.
2. Перейдем в строку формул.
3. Введем знак 0.
4. Установим курсор на ячейку А9 (в ней содержится наш заголовок) и нажмем Enter
5. В контекстно-зависимом меню редактирования названия выберем Форматировать название диаграммы, Шрифт, Arial Cyr, полужирный, 12.

24.5.3. Изменение цвета секторов на "узоры"

Так как при печати на черно-белом принтере цвет секторов не будет виден, то лучше использовать "узоры". Для этого надо произвести следующие действия:
1. Выделим сектор диаграммы;
2. Вызовем контекстно-зависимое меню и выберем Ф орматировать элемент данных=Вид=Закраска области=Узор;
3. Подберем узоры всем секторам.

Для лучшего представления легенды на нашей диаграмме сделаем следующее:
1. Выделим легенду и вызовем контекстно-зависимое меню.
2. Подберем шрифт, вид и размещение таким образом, чтобы легенда красиво выглядела на графике.

Возможно изменение размеров (данной диаграммы, для этого:
1. Выделим область диаграммы с помощью клавиш управления курсором.
Рамка охватывает рисунок диаграммы. Размер ее можно изменить, также как и область расположения и размер всего рисунка с диаграммой.
2. “Буксируя” черные квадратики, подберем оптимальный размер области диаграммы.

Так же, как и при подготовке к печати документов редактора Word, перед печатью рекомендуется просмотреть диаграмму.

Как быть, если нам необходимо построить графики нескольких функций? Например: Y1=2х-1, Y2=x+1, Y=10x(Y1/Y2). Для построения обыкновенных графиков функций у=f(x) используется тип диаграммы XY-точечная. Этот тип диаграммы требует два ряда значений: Х-значения должны быть расположены в левом столбце, а Y-значения - в правом. На одной диаграмме можно построить несколько графиков функций. Эта возможность используется для проведения сравнительного анализа значений У при одних и тех же значения вставить X, а также для графического решения систем уравнений с двумя переменными.
Воспользуемся таблицей, созданной на уроке N 22. На одной диаграмме построим три совмещенных графика: Y1=2х-1, Y2=2x+l, Y=10x(Y1/Y2). Для этого:
1. Загрузим файл Ex21.xls.
2. Снимем защиту с листа.
3. Переместим вспомогательную таблицу под основную, начиная с ячейки В27.
4. Щелкнем по кнопке Мастер диаграмм и выберем область для построения диаграммы Н2: К28. Рассмотрим построение диаграммы по шагам:
На 1-м шаге укажем ячейки В4: В24 (Х-значения) и D3:F24 (Y- значения и заголовки для легенды). Обратите внимание, что указываются 3 столбца (3 ряда Y-значений), так как мы хотим построить 3 совмещенных графика. Для построения одного графика необходим 1 столбец Y-значений.
На 2-м шаге укажем тип XY-точечная.
На З-м шаге выберем формат 6.
На 4-м шаге исправим неправильный образец диаграммы. Отведем один столбец для данных по оси X и одну строку для текста легенды.
На 5-м шаге добавьте название диаграммы Совмещенные графики. Укажите название по оси X-<Х, название по оси Y-<Y. Проведем форматирование области диаграммы:
1. Подберем оптимальный размер области диаграммы так, чтобы таблица значений и график размещались на одном листе в ландшафтной ориентации.
2. Вызовем контекстно-зависимое меню и выберем Форматировать область диаграммы=Рамка пользовательская=Закраска области=Узоры.
3. Выберем толщину рамки и узор. Установим маркеры на графике:
1. Выделим линию графика и вызовем контекстно-зависимое меню Форматировать=Ряд=Вид=Маркер пользовательский=Стиль.
2. Выберем необходимый маркер.
Обратите внимание, что.маркеры в легенде автоматически изменяются
После этого можно отредактировать названия осей X н Y, для этого:
1. Выделим название оси Y и (“перетащим” его на традиционное место обозначения оси.
2. Щелкнем правой кнопкой мыши на названии оси Y. В меню редактирования названия оси выберем Форматировать название оси Выравнивание=Ориентация горизонтальная.
3. Переместим название оси X. Проведем форматирование области построения диаграммы:
1. Выделим область построения диаграммы.
2. Выберем в контекстно-зависимом меню Форматирование области построения=Рамка пользовательская=Закраска области автоматическая.
3. Выберем толщину рамки и цвет для закраски. Сохраняем файл под новым именем Ex44.xls. Подготовим таблицу и график к печати: выберем ландшафтное расположение, уберем сетку и колонтитулы. Распечатаем таблицу и график на одном листе.

ИСПОЛЬЗОВАНИЕ ЭЛЕКТРОННОЙ ТАБЛИЦЫ EXCEL ДЛЯ ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ

Электронная таблица выполняет не только функцию автоматизации расчетов. Она является очень эффективным средством численного моделирования ситуации или объекта, для математического описания которых, т.е. построения математической модели, используется ряд параметров. Часть этих параметров известна, а часть рассчитывается по формулам. Меняя в различных сочетаниях значения исходных параметров, можно наблюдать за изменением расчетных параметров и анализировать получаемые результаты. Электронная таблица производит такие расчеты быстро и без ошибок, предоставляя в считанные минуты множество вариантов решения поставленной задачи, на основании которых вы выберете наиболее приемлемый.
Попробуем решить следующую задачу: Какова будет численность населения города “А” в начале третьего тысячелетия?
Сразу ясно, что задачу не решить, если не знать, как со временем будет меняться численность населения города “А”, т. е. необходимо иметь функцию, выражающую зависимость численности населения от времени. Обозначим эту функцию f(t). Но такая функция неизвестна, так как народонаселение зависит от многих факторов: экологии, состояния медицинского обслуживания, морали, права и даже от политической обстановки. Но, обобщив демографические данные, можно указать общий вид функции f(t): 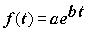(1), где коэффициенты а, b - свои для каждого города и государства, е - основание натурального логарифма. Эта формула лишь приближенно отражает реальность. Однако слишком большая точность и не нужна. Хорошо, если численность населения будет спрогнозирована с точностью до десятков тысяч.
Как же определить а и b? Идея состоит в следующем: хотя а и b неизвестны, значение функции f(t) можно получить из статистического справочника. Зная t и f(t), можно приближенно подобрать а и b так, чтобы теоретические значения, вычисленные по формуле (1), не сильно отличались от данных справочника (т. е. максимальное отклонение теоретических результатов от фактических данных не должно быть слишком большим). Каждое из отклонений - это модуль разности двух чисел: фактического и соответствующего теоретического значений f(t). Максимальное отклонение называют погрешностью. Необходимо найти такие а и b, чтобы погрешность была наименьшей. Итак, математическая модель процесса изменения численности населения такова.
Предполагается, что:
1) Зависимость численности населения от времени выражается формулой .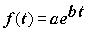
2) а=const и b=const следует считать справедливым лишь для не очень большого промежутка времени (например, 40 лет).
3) Значения а и b можно найти с достаточной точностью, минимизировав погрешность.
Исходные данные: Будем считать, что у нас имеются сведения из статистического справочника о численности населения (в тыс. человек) за период с 1960 по 1996 г. (60 <= 1 <= 96). Результаты:
1) значения а и b,
2) численность населения города “А” в 2000 г. (t = 100). Кроме того, установлена связь между исходными данными и результатами: сначала надо найти а и b, минимизируя погрешность, а затем при этом а и b вычислить значение f(100).
Итак, математическая модель составлена. Использование электронной таблицы освобождает от составления программы. Нужно только определенным образом записать в таблицу исходные данные и математические соотношения, входящие в модель. После этого можно начать процесс численного моделирования исследуемой ситуации, т. е. подбор коэффициентов а и b в формуле (1), а затем определение численности населения. Заполним таблицу. Сделаем заголовок. Заполним шапку таблицы. Столбцы А и В отведем под коэффициенты а и b соответственно. Коэффициенты а и b не изменяются с течением времени, значит, во всех ячейках столбцов А и В должны быть записаны одни и те же числа. В столбец С занесем значения t с 1960 г. В столбец D занесем взятые из справочника значения численности населения города “А” (с 1960 г.) в тыс.чел. В столбец Е занесем формулу =А?ЕХР(ВС). В столбец F занесем формулу =ABS(E-D). Это модуль разности теоретического и фактического значений функции f.
Для подсчета максимальной погрешности по столбцу G в любую свободную ячейку этого столбца введем функцию max. Всякий раз после пересчета чисел в столбце F в этой клетке будет записано максимальное из чисел этого столбца. Следующим шагом будет подбор коэффициентов а и b. Поместим в столбцы А и В какие-нибудь числа. При этом заполнятся столбцы Е и F, причем погрешность, появившаяся в ячейках столбца F, скорее всего очень велика. Изменим коэффициенты а и b так, чтобы погрешность уменьшилась. Для этого лучше всего составить алгоритм поиска а и b (примерный). В составлении этого алгоритма нам поможет анализ формулы (1). Сделав погрешность малой (на Ваш взгляд), подставьте в свободную ячейку столбца С число 100. В соответствующей ячейке столбца Е появится искомое число.
Теперь построим на одной диаграмме графики роста численности населения: на основе статистических и теоретических данных (с подобранными вами коэффициентами а и b.

Дата добавления: 2014-01-06