Def. Взвешенный вершинный граф – это взвешенный орграф, в котором отсутствует вес дуг

Сети.

Теория графов

Теория графов – область дискретной математики, к которой существует топологический подход к изучению объектов. Предмет теории графов – граф и его обобщения (гиперграф, сеть, отображение топологических объектов, отношения). Графы и их обобщения служат инженерным языком.

Пример. Задача о Кенигсбергских мостах. Обойти все четыре части суши, пройдя по каждому мосту один раз, и вернуться в исходную точку.

N= ‹V, E ›

Сетью называется пара множеств, в которых V – это непустое множество вершин.

Е=Е₀ È Е₂ È Е₃ È … È Е_m, где Е непустое семейство множества вершин. Принято Е₀ называть полюсом сети. Термин семейство частей множества вершин означает, что ребра семейства могут повторяться, т.е. быть кратными, а также могут быть помеченными. Часто ребра обозначают строчными буквами, е – это ребро, трактуемое как множество вершин: е_i Í V

_

e_i – это дуга, трактуемая как картеж.

Способы задания сети.

Рассматривают 3 наиболее часто применяемых задания:

10. теоретико – множеств.

11. графический (схемы связанных областей плоскости).

12. матричный (весовая матрица инцидентности).

Пример:

N= ‹V,E ›, N - сеть

Пусть мощность множества вершин равна |V| = 7

Е₀ = ‹V_1, V_2, V₃ ›

E₁ = ‹V₁, V₃, V3, V₄, V₅›

E₂ = ‹ V₄, V₄, V₅, V₆ ›

E₃= E₄ = ‹V₂, V₄ ›

E₅= ‹V₂, V₅, V₆, V₇ ›, E3 и E4 – кратные ребра (параллельные ребра)

Графическим представлением задания сетей может быть схема.

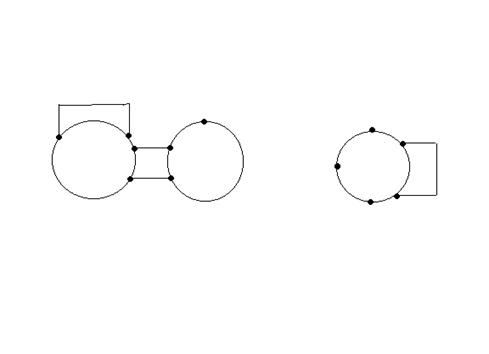
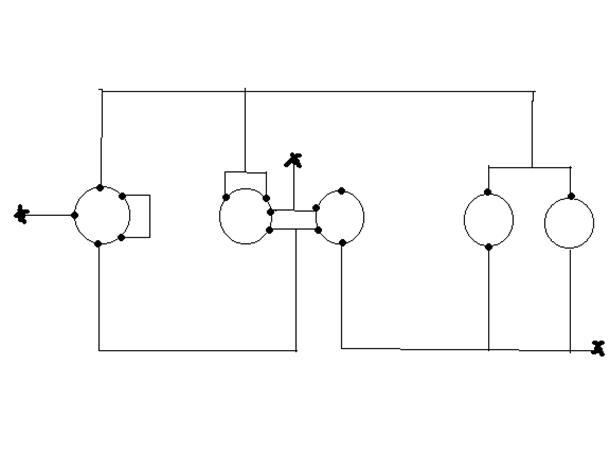
Весовая матрица инцидентности имеет вид:

E0	_ e1	_ e2	_ e3	_ e4	_ e5
						V1
						V2
						V3
						V4
						V5
						V6
						V7

f: V´ E® {0,1.2}

Классификация сетей

1) N = ‹V, E ›

Гиперграф – это сеть, в которой число полюсов представляет собой пустое множество. Н= ‹ V, E ›, т.е. сеть, в которой Е – пустое множество,

U E_i =V

_ __ ___

§ S = ‹ s, C_v, C_n ›, |e_i | = 2; i = 1,n

C_v: V ® R⁺ , C_n: V ® R⁺

Орграф – ориентированный граф; неограф – неориентированный граф.

Взвешенный орграф с выделенными полюсами – это такая сеть, в которой ребра (дуги) состоят из 2-х вершин, а вершины и ребра имеют вес.

Замечание 1

Для бинарных ребер(дуг) приняты обозначения u_i (u_i)

Замечание 2

Множество бинарных множеств (дуг) обозначают: U (U)

Замечание 3

Для орграфа и неографа приняты обозначения:

U = { U₁, U₂,…,U_n}

__ __ __ __

U = { U₁, U₂,…,U_n}

Замечание 4

Орграф сокращение ориентированного графа. Неограф сокращение неориентированного графа.

Типами сети будут частные случаи гиперграфа и взвешенного орграфа с выделенными полюсами. Частные случаи гиперграфов – сеть без выделенных полюсов. Гиперграф, ребра которого суть нечеткого подмножества вершин, называют нечетким гиперграфом. H = ‹ V, E ›. Множество всегда является четким.

Связный гиперграф, все ребра которого есть 2-х элементные подмножества (четкие или нечеткие) называются неориентированными графами (соответственно, неориентированный четкий или неориентированный нечеткий граф).

Замечание 1

Неограф – нерефлексивное, симметричное отношение на множестве вершин. Неограф – частный случай гиперграфа. Связный гиперграф, все ребра которого есть 2-х компонентные картежи (дуги), называются асимметричным псевдографом.

Замечание 2.

Дуга называется петлей.

Замечание 3.

Псевдоорграф, в котором отсутствуют петли называют орграфом.

Замечание 4.

Матроидом М= ‹V, J ›

Называется гиперграф, ребра которого являются набором независимых подмножеств J (это булеан, где булеан задан количеством вершин).

Def. Взвешенный (помеченный) орграф – орграф без выделенных полюсов, каждая дуга и вершина которого взвешены.

Транспортной сетью называется система с 2-мя выделенными полюсами (исток и сток), при этом исток не может совпадать со стоком, а функция веса ребер(дуг) интерпретируется как функция пропускных способностей дуг.

Сеть Петри – взвешенный вершинный орграф, множество вершин которого есть объединение подмножеств вершин и подмножеств вершин перехода. Областью определения весовой функции является множество вершин позиций, помеченных натуральными числами.

 = ‹T, P, C_v ›

TÈ P = V; TÇ P = Æ

Дата добавления: 2014-01-06