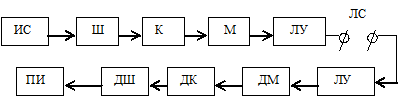КАТЕГОРИИ: Главная Случайная страница Познавательное Новые статьи Контакты Заказать работу Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)

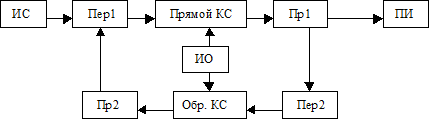
Определение системы передачи информации ОСНОВНЫЕ ПОНЯТИЯ КАНАЛЫ ПЕРЕДАЧИ ИНФОРМАЦИИ Теоремы о потоках в транспортной сети. Теоремы об изоморфизме графов. Теоремы о планарности графа. § Всякий подграф планарного графа планарен § Граф планарен тогда и только тогда когда, когда каждая его связная компонента планарный граф. § Теорема Эйлера: Для каждого графа справедлива формула Эйлера: ½ V½ -½ U½ + ½ é ½ =2 § Для связного планарного графа ½ U½ £ 3½ V½ -6 при½ V½ ³ 3 (это вытекает из равенства ½ U½ =3½ V½ -6 для максимально плоского графа) § Теорема Фари: Для любого планарного графа существует плоское представление, в котором все ребра - прямолинейные отрезки § Теорема о "раскраске" графа: Для всякого планарного графа его хроматическое число g (s) £ 5(возможно и g (s) £ 4- это так называемая проблема о четырех красках, но то, что граф является 4- х- хроматическим всего лишь предположение). § Критерий планарности графа Понтрягина – Куратовского: Граф планарен тогда и только тогда, когда он не содержит подграфов, гомоморфных К5 или К3,3 § Теорема Кенга: Граф является двудольным тогда и только тогда, когда он не имеет циклов нечетной степени (т.е. карта допускает раскраску в два цвета тогда и только тогда, когда каждая вершина имеет четную степень). или Граф может быть представлен в виде двудольного графа, если все его циклы имеют четкое число ребер. § Два графа являются изоморфными, если они имеют одни и те же матрицы инцидентностей с точностью до перестановок строк и столбцов. § Теорема о максимальном истоке и минимальном разрезе: Величина каждогостационарного потока j (U) для заданной транспортной сети из q(истока) в S(сток) не превышает пропускной способности минимального разреза, разделяющего q и S, причем существует поток, достигающий этого значения (эта теорема доказана Фордом и Фалкерсоном) т.е. max j S= min S cn(Ui) где j S- поток в стоке S ?(U)-множество дуг минимального разреза транспортной сети c(Ui)- пропускная способность дуги Vi транспортной сети (³ 0) Пример: j q=2+3+1=6 j s= -(2+3+1)= -6     Имеем:   j smax =divVq= 4+5+2= 11 j smin= div Vs= -(3+4+4)= -11     § Теорема о целочисленности потока в транспортной сети: Если пропускная способность c(U) дуг Vi транспортной сети целочислена, то существует максимальный стационарный исток j S max, который целочисленен. Примечание: Теорема о максимальном потоке и минимальном разрезе позволяет получить как следствия следующие теоремы: § Теорема о максимальном паросочетании в двудольном графе ‹V’, V", U›: max(| B| -| é B|) = 0 Пример:

Система передачи дискретной информации (СПДИ) - основной элемент автоматизированных систем управления технологическими процессами (АСУ ТП), информационно-управляющих систем (ИУС) и любых других систем, в которых существуют процессы передачи и преобразования информации.

На рис.1.1 приведена обобщенная структурная схема СПДИ.

ИС – источник сообщений; ПИ – получатель информации; ИО – источник ошибок; Пер.1, Пер.2 – передатчики сообщений; Пр.1, Пр.2 – приемники сообщений; КС – канал связи

Рис.1.1

СПДИ - совокупность передатчиков, приемников и каналов, обеспечивающих обмен сообщениями между двумя пунктами или передачу сообщения от одного пункта к другому. Сообщения в прямом канале и в обратном канале искажаются под воздействием помех. Искажения рассматриваются как внесение ошибок в передаваемую информацию. Одной из основных задач является построение модели источника ошибок.

Поток сообщения от ИС следует рассматривать как случайный поток.

Каналом передачи информации называют совокупность устройств, обеспечивающих передачу сигналов от одного пункта к другому. При построении СПДИ канал является заданным звеном, ИС и ПС согласуются с КС посредством передатчика и приемника.

ИО вызывает искажения информации. Чтобы восстановить искаженную информацию, необходимо применение кодирования.

КС – это линия связи, на концах которой находится оборудование, производящее оконечную обработку данных преобразователем сообщений (модемы, фильтры и усилители).

Передатчик – это устройство, которое преобразует сообщение X(t) в сигнал S(t).

Приемник – это устройство, которое преобразует сообщение S^*(t) в сообщение X^*(t).

На рис.1.2 приведена структурная схема однонаправленного КС.

Ш – шифратор, К – кодер, М – модем, ЛУ – линейное устройство, ЛС – линия связи, ДМ – демодулятор, ДК – декодер, ДШ - дешифратор

Рис.1.2

Шифратор преобразует сообщение в безызбыточный код. Кодер преобразует безызбыточный код в помехозащищенный код, добавляет контрольные символы. Модулятор преобразует сигналы в форму, удобную для передачи по КС. На выходе модулятора будет аналоговый сигнал. Демодулятор преобразует аналоговый сигнал в дискретный. Декодер декодирует код и корректирует ошибки. На выходе дешифратор преобразует код в сообщение.

Кодер образует устройство защиты ошибок (УЗО) передатчика, а декодер – УЗО приемника. Модулятор и ЛУ образуют устройство преобразования сигналов (УПС) передатчика, а ЛУ и демодулятор – УПС приемника.

Отождествление принимаемого элементарного сигнала с определенным кодовым символом выполняется в первой решающей схеме (выход демодулятора). Преобразование кодовых символов в сообщение осуществляется с помощью второй решающей схемы (выход дешифратора).

Дата добавления: 2014-01-06; Просмотров: 988; Нарушение авторских прав?; Мы поможем в написании вашей работы!