Способы воспроизведения сигнала

Способы воспроизведения сигнала характеризуются [8, 11]: видом базисных функций и формой дискретного представления сигнала (видом координат), определяющими тип аппроксимирующего полинома и характер аппроксимации; числом отсчетов аппроксимирующего ряда.

При ортогональном представлении сигнала выбирается критерий среднеквадратичного приближения. Координаты разложения a_k определяются по формуле

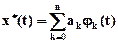. (2.1)

Представление сигнала в виде ряда (2.1) является оптимальным, т.к. он минимизирует число координат при заданной степени полинома и величине допустимой среднеквадратичной ошибки.

Для ортогонального представления сигнала процесс временной дискретизации сводится к вычислению коэффициентов ряда Фурье. Однако это имеет недостаток, обусловленный ограниченной точностью вычисления коэффициентов Фурье и сложностью устройства временной дискретизации.

В технике распространены неортогональные представления сигналов в виде линейно независимых базисных функции вида

или .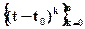

Тогда ряд (2.1) принимает вид

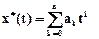(2.2.)

или

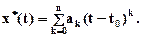(2.3)

Из теории приближений известно, что если разложение x(t) функции в степенной ряд (2.2) сходится при n®¥, то оно является разложением в ряд Тейлора

,

где x^k(t₀) - k -я производная x(t) в точке t₀. Таким образом, для нахождения координат a₀=x(t₀) и a_k=x^k(t₀)/k! необходимо знать x(t₀) и x^k(t₀).

Приближение с помощью полиномов Тейлора основано на представлении (экстраполяции) возможного поведения сигнала x(t) на интервале аппроксимации по коэффициентам a_i, i=0,1,…,n, соответствующим начальному моменту времени t₀. Сигнал воспроизводится без задержки.

Выбор в качестве координат значений сигнала x(t_k) при условии совпадения значений аппроксимирующего полинома (2.3) с функцией x(t_k) в точках t_k, называемых узлами интерполяции, приводит к интерполирующему полиному Лагранжа

.

2.4.1. Выбор шага дискретизации по временным характеристикам сигнала. В.А. Котельниковым доказана теорема для функции с ограниченным спектром, согласно которой функция полностью определяется дискретным множеством своих значений (отсчетов), взятых с частотой счета F₀=2f_m, где f_m - максимальная частота в спектре S(jw) сигнала x(t).

Сигнал x(t) может быть восстановлен без погрешностей по точным значениям выборок x(t_k) в виде

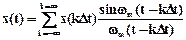. (2.4)

Интерполяционный ряд (2.4) называется рядом Котельникова.

Сигнал x(t) - непрерывная функция и имеет ограниченный спектр, т.е.

,

удовлетворяющий условию S(jw)=0 при |w|>w_m, т.е. в представлении сигнала рядом Фурье

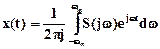. (2.5)

Рассматривая S(jw) как функцию частоты, период которой равен величине 2w_m, можно разложить эту функцию в ряд Фурье на интервале [-w_m,w_m]:

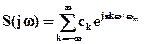, где (2.6)

Сравнивая формулы (2.5) и (2.6), видим, что они совпадают с точностью до постоянного множества Dt=p/w_m, если принять t=-kDt, т.е.

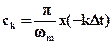, тогда.

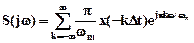Подставим это выражение в (2.5), изменив при этом знак с учетом того, что суммирование производится по всем отрицательным и положительным значениям k. Учитывая сходимость ряда и интеграла Фурье, изменим порядок операций интегрирования и суммирования

, (2.7)

причем . (2.8)

Подставив (2.8) в формулу (2.7), получим формулу (2.4).

Таким образом, непрерывная функция x(t) с ограниченным спектром может быть точно представлена отсчетами x(kDt), взятыми через равные интервалы Dt=1/2F_m=p/w_m.

Функцию 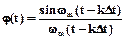называют функцией отсчетов.

Теорема Котельникова сохраняет свой смысл применительно к случайным процессам с ограниченным спектром. Если известна автокорреляционная функция R_x(t), то шаг дискретизации выбирается равным интервалу корреляции

.

Реальные сигналы ограничены и спектр их бесконечен. Тогда ряд Котельникова дает приближенное математическое описание сигнала с неограниченным спектром.

Энергетический критерий имеет вид

,

где DЕ – энергия ошибки d(t) (погрешность аппроксимации)

На практике вводят ограничение f_m и рассматривают конечный спектр. Функция может быть представлена числом отсчетов N=t_m/Dt. Исходный сигнал восстанавливается полиномом Котельникова с некоторой погрешностью, т.е. полином следует рассматривать как аппроксимирующую функцию x^*(t):

.

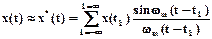При крутом спаде спектра оценка относительной среднеквадратичной погрешности определится

,

где Р – мощность сигнала, причем

,

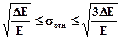где Е – полная энергия сигнала определится по формуле

.

2.4.2. Выбор шага дискретизации по производным сигнала. Рассматривается функция x(t), непрерывная на интервале наблюдения и имеющая ограниченное число конечных и непрерывных производных. Опишем x(t) аппроксимирующим полиномом

,

где R_n+1(t) – остаточный член, определяющий функцию погрешности аппроксимации d(t)=x(t)-x^*(t)= R_n+1(t).

На практике в качестве аппроксимирующей функции обычно используют экстраполирующий полином Тейлора или интерполирующий полином Лагранжа. Критерий приближения – равномерный и максимальная погрешность воспроизведения определится по формуле

max|d(t)|=max|R_n+1(t)|=|d_m|£A(Dt,M_n+1),

где A(Dt,M_n+1) - оценка сверху, зависящая от шага Dt и M_n+1 - модуля-максимума (n+1) -й производной сигнала.

Решение уравнения A(Dt,M_n+1)=d_Д, где d_Д – допустимая погрешность воспроизведения, относительно Dt дает формулу для расчета шага дискретизации.

Погрешность воспроизведения оценивается первым отброшенным членом полинома, т.е. d(t)»a_n+1j_n+1(t).

Рассмотрим экстраполяцию сигнала полиномом Тейлора нулевой степени (ступенчатая экстраполяция), n=0, x^*(t)»x(t₀).

На рис.2.2 приведена иллюстрация выбора шага дискретизации.

Погрешность оценим первым отброшенным членом ряда - d(t)»x⁽¹⁾(t₀)(t-t₀). Очевидно, что это уравнение прямой (см. рис.2.2). Тогда x(t)»x(t₀)x⁽¹⁾(t₀)(t-t₀). Так как t-t₀ максимально при t=t₁,то

.

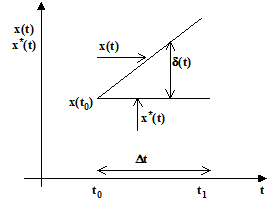
Рис.2.2

Погрешность будет принимать наибольшее значение при максимуме первой производной x⁽¹⁾, тогда

,

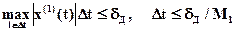где М₁ – модуль-максимум первой производной.

На рис.2.3 приведена иллюстрация экстраполяции сигнала полиномом Тейлора при n=0.

Рис.2.3

Рассмотрим экстраполяцию сигнала полиномом Тейлора первой степени (линейная экстраполяция): n=1, x^*(t)»x(t₀)+x⁽¹⁾(t₀)(t-t₀).

Сигнал будет представлен в виде ряда

.

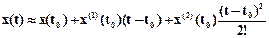На рис.2.4 приведена иллюстрация выбора шага дискретизации.

Рис.2.4

Погрешность воспроизведения сигнала определится по формуле

. Тогда , где М₂ - модуль-максимум второй производной. На рис.2.5 приведена иллюстрация экстраполяции сигнала полиномом Тейлора при n=1.

Рис.2.5

Рассмотрим интерполяцию сигнала полиномом Лагранжа нулевой степени: n=0, x^*(t)»x(t^*). Отсчет берется в любой точке t^* интервала Dt. Отсчет лучше брать в середине интервала, тогда x^*(t)=x(t^*),

На рис.2.6 приведена иллюстрация выбора шага дискретизации.

Ориентируясь на наихудший случай, т.е. на наибольшее значение x⁽¹⁾ на интервале наблюдения, получим

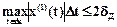. Тогда .

Задержка воспроизведения сигнала составит половину шага дискретизации. На рис.2.7 приведена иллюстрация интерполяции сигнала полиномом Лагранжа при n=0. Данная интерполяция называется ступенчатой интерполяцией.

Рис.2.6

Рис.2.7

Рассмотрим интерполяцию сигнала полиномом Лагранжа первой степени: n=1, . На рис.2.8 приведена иллюстрация выбора шага дискретизации.

Данная интерполяция называется линейной, а сигнал описывается с требуемой точностью полиномом Лагранжа второй степени:

.

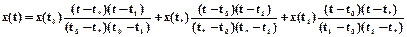Полагая t₀=0 и вводя t^’=t-t₀, оценим погрешность воспроизведения: d(t^’)=x(t^’)-x^*(t^’)=Bt^’(t^’-t₁), t^’ÎDt, где

.

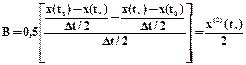Рис.2.8

Погрешность d(t^’) примет наибольшее значение при t^’=t_*^’=Dt/2, тогда

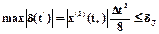. Следовательно, .

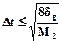На рис.2.9 приведена иллюстрация интерполяции сигнала полиномом Лагранжа при n=1.

2.4.3. Выбор шага дискретизации по вероятностным характеристикам сигнала. Рассматривается сигнал - случайная стационарная функция. Принята равномерная временная дискретизация, ступенчатая экстраполяция и среднеквадратичный критерий приближения. На рис.2.10 приведена иллюстрация выбора шага дискретизации.

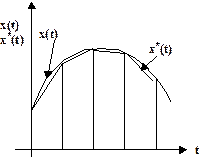
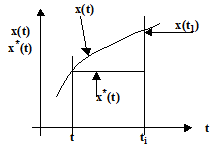
Рис.2.9 Рис.2.10

Среднеквадратичная ошибка воспроизведения в конце участков аппроксимации t_i, 1=1,2,3,…, определится

s²=M{[x(t_i)-x^*(t)]²}=M{[x(t_i)-x(t_i-Dt)]²}.

При ступенчатой экстраполяции x^*(t)=x(t_i-Dt)=x(t_i). Учтем, что

M{x²(t_i)}=M{x²(t_i-Dt)}=D_x+m_x²; M{x(t_i)x(t_i-Dt)}=B_x(Dt)+m_x², тогда s²=2[D_x - B_x(Dt)].

Шаг дискретизации определится решением уравнения s²³2[D_x - B_x(Dt)].

Рассмотрим линейную интерполяцию. Воспроизводящая функция имеет вид

.

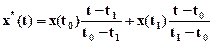Выполним следующие преобразования:

.

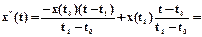
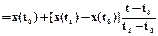Пусть 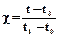, тогда x^*(t)=(1-c)x(t₀)+cx(t₁).

Среднеквадратичная ошибка воспроизведения определится

s²=M{[x(t)-x^*(t)]²}=M{[x(t)-(1-c)x(t₀)-cx(t₁)]}.

Учитывая, что M{x²(t)}=D_x+m_x²=М{x²(t₀)}=М{x²(t₁)}; M{x(t)x(t₀)}=B_x(t-t₀)+m_x², M{x(t)x(t₁)}=B_x(t-t₁)+m_x², M{x(t₀)x(t₁)}=B_x(t₁-t₀)+m_x², t₁-t₀=Dt, получим

s²=D_x[1-(1-c)²+c²]-2(1-c)B_x(t-t₀)-2cB_x(t-t₁)+2c(1-c)B_x(Dt).

Среднеквадратичная ошибка воспроизведения будет наибольшей в середине участка аппроксимации, т.е. при c=0,5, t-t₀=Dt/2, t-t₁=Dt/2. Тогда

.

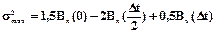Для заданного значения средней погрешности s_Д величина щага дискретизации должна выбираться из условия

.

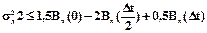Дата добавления: 2014-01-06