Проверочная матрица

Преобразуем соотношение (3.3) к виду

. (3.6)

Соотношениям (3.3) и (3.6) должны удовлетворять все символы кодовых комбинаций, поэтому эти соотношения называют проверочными.

Ели записать правило (3.6) формирования каждого контрольного элемента в виде последовательностей из нулей и единиц, где единицы на позициях, соответствующих информационным элементам, указывают, какие информационные разряды участвуют в образовании того контрольного элемента, на позиции которого в последовательности стоит единица, то получим k последовательностей. Запишем эти последовательности в прямоугольную таблицу размерности k´n, называемую контрольной или проверочной матрицей

.

В первой строке матрицы H_k,n записано уравнение для формирования первого контрольного элемента:

b₁q₁₁Å b₂q₂₁Å b₃q₃₁Å…Åb_mq_m1Åc₁=0.

Во второй строке матрицы H_k,n записано уравнение для формирования второго контрольного элемента:

b₁q₁₂Å b₂q₂₂Å b₃q₃₂Å…Åb_mq_m2Å c₂=0.

В третьей строке матрицы H_k,n записано уравнение для формирования третьего контрольного элемента:

b₁q₁₃Å b₂q₂₃Å b₃q₃₃Å…Åb_mq_m3Å c₃=0.

В k -й строке матрицы H_k,n записано уравнение для формирования k -го контрольного элемента:

b₁q_1kÅ b₂q_2kÅ b₃q_3kÅ…Åb_mq_mkÅ c_k=0.

Пример. Код (6,3) можно построить с помощью образующей матрицы

.

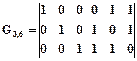Матрица 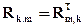имеет вид

.

Проверочная матрица

Уравнения формирования контрольных элементов: b₂Åb₃Åc₁=0, b₁Åb₃Åc₂=0, b₁Åb₂Åc₃=0.

Если информационная последовательность имеет вид 101, то c₁ =1, c₂ =0, c₃ =1, а кодовая комбинация – 101101.

Таким образом, задание проверочной матрицы H_k,n является одним из способов описания группового кода (можно формировать кодовые комбинации).

Образующая и проверочная матрицы связаны проверочным соотношением

.

Если принимаемая кодовая комбинация b^* принадлежит кодовому множеству, то для нее выполняется соотношение (3.3), а матричное произведение

. (3.7)

Выполнение условия (3.7) свидетельствует об отсутствии ошибки в принятой кодовой комбинации b^*.

Если при передаче возникла ошибка e, то b^*=bÅe и тогда

. (3.8)

Двоичная последовательность 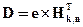называется опознавателем (корректором или синдромом) ошибки. Опознаватель ошибки представляет собой k разрядное двоичное число d₁d₂,…,d_k. Опознаватель ошибки можно также получить, если применить к принятой кодовой комбинации b^* систему проверочных соотношений (3.6)

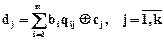. (3.9)

Если все элементы d_i=0 (D=0), то в принятой кодовой комбинации ошибок нет.

Пример. Проверочная матрица кода (6,3)

.

Уравнения формирования контрольных элементов: b₂Åb₃Åc₁=0, b₁Åb₃Åc₂=0, b₁Åb₂Åc₃=0. Пусть b^* =110110 не содержит ошибок. Результаты проверок следующие: d₁ =1Å0Å1=0, d₂ =1Å0Å1=0, d₃ =1Å1Å0=0. Тоже можно получить в результате умножения 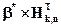=(1х0Å1х1Å0х1Å1х1Å1х0Å0х0Å, 1х1Å1х0Å0х1Å1х0Å1х1Å0х0, 1х1Å1х1Å0х0Å1х0Å1х0Å0х1)=(000).

Пусть e =000100, т.е. b^* =110010, тогда d₁ =1Å0Å0=1, d₂ =1Å0Å1=0, d₃ =1Å1Å0=0. Таким образом, D =100 фиксирует наличие ошибки в принятой кодовой комбинации.

Дата добавления: 2014-01-06