Сумма и произведение событий. Противоположные события

Классическое определение вероятности

Вероятность - одно из основных понятий теории вероятностей. Существует несколько определений этого понятия.

Дадим ряд вспомогательных определений.

Определение 1. События называют несовместными, если появление одного из них исключает появление других событий в одном и том же испытании.

Например, при бросании монеты появление «герба» исключает появление «надписи».

Определение 2. Несколько событий образуют полную группу, если в результате испытания появится хотя бы одно из них.

В частности, если события, образующие полную группу, попарно несовместны, то в результате испытания появится одно и только одно из этих событий.

Определение 3. События называются равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другое.

Например, появление «герба» и «надписи» при бросании монеты – равновозможные события.

Рассмотрим пример. Пусть в урне содержится 6 оди­наковых, тщательно перемешанных шаров, причем 2 из них – красные, 3 – синие и 1 – белый. Очевидно, возмож­ность вынуть наудачу из урны цветной (т. е. красный или синий) шар больше, чем возможность извлечь белый шар. Можно ли охарактеризовать эту возможность числом? Оказывается, можно. Это число и называют вероятностью события (появления цветного шара).

Таким образом, вероятность есть число, характеризующее степень возможности появления события.

Отношение числа благоприятствующих событию А эле­ментарных исходов к их общему числу называют вероят­ностью события А и обозначают через Р(А). В рассмат­риваемом примере всего элементарных исходов 6; из них 5 благоприятствуют событию А. Следовательно, вероят­ность того, что взятый шар окажется цветным, равна Р (А) = 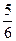. Это число и дает ту количественную оценку степени возможности появления цветного шара, которую мы хотели найти.

Определение. Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу.

Итак, вероятность события А определяется формулой:

Р(А) = ,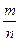

где т - число элементарных исходов, благоприятствую­щих А;

п - число всех возможных элементарных исходов испытания.

Здесь предполагается, что элементарные исходы не­совместны, равновозможны и образуют полную группу.

Из определения вероятности вытекают следующие ее свойства:

Свойство 1. Вероятность достоверного события равна единице.

Действительно, если событие достоверно, то каждый элементарный исход испытания благоприятствует собы­тию. В этом случае т = п, следовательно,

Р(А) = 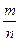= = 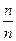1.

Свойство 2. Вероятность невозможного события равна нулю.

Действительно, если событие невозможно, то ни один из элементарных исходов испытания не благоприятствует событию. В этом случае т = 0, следовательно,

Р(А) = 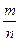= = 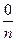0.

Свойство 3. Вероятность случайного события есть положительное число, заключенное между нулем и еди­ницей, т.е. 0 <Р(А)<1.

Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных исходов испы­тания. В этом случае 0 < т < п, значит, 0<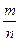<1, следовательно, 0<Р(А)<1.

Итак, вероятность любого события удовлетворяет двой­ному неравенству:

0≤ Р(А) ≤1.

Определение. Суммой А+В двух событий А и В называют событие, состоящее в появлении хотя бы одного из событий (т.е. или А, или В, или оба вместе).

Например, если из орудия произведены два выстрела и А – попадание при первом выстреле, В – попадание при втором выстреле, то А+В – попадание при первом выстреле, или при втором, или в обоих выстрелах.

Если два события А и В – несовместные, то А+В – событие, состоящее в появлении одного из этих событий, безразлично какого.

Определение. Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении этих событий.

Например, если А – деталь годная, В – деталь окрашенная, то АВ – деталь годная и окрашена.

Определение. Противоположным событию А называется событие 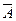, которое происходит только тогда, когда не происходит событие А.

Например, при выстреле по цели попадание и промах – противоположные события. Часто вероятности противоположных событий обозначают р и q.

События А и 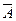образуют полную группу.

Теорема. Сумма вероятностей противоположных событий равна единице: Р(А)+Р(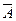)=1.

Задача. Вероятность того, что день будет дождливым равна 0,7. Найти вероятность того, что день будет ясным.

Решение. События «день дождливый» и «день ясный» – противоположные, поэтому искомая вероятность q=1– р=1– 0,7=0,3.

Дата добавления: 2014-01-06