Системы линейных уравнений

Система линейных алгебраических уравнений (или линейная система) имеет вид:

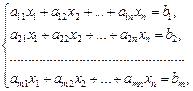(13.7)

где a_ij и b_j – заданные числа.

Эту систему можно записать в матричной форме

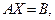(13.8)

где 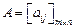– матрица системы, состоящая из коэффициентов a_ij,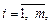 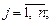B – матрица-столбец свободных элементов b_j, 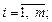X – матрица-столбец неизвестных, т. е. такая, которая обращает матричное уравнение (13.8) в равенство (является решением этого уравнения).

Решением системы (13.7) называется упорядоченная совокупность 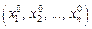n чисел, которые после подстановки в уравнения системы вместо соответствующих переменных обращают каждое уравнение системы в верное числовое равенство.

Система (13.7) называется совместной, если у нее существует хотя бы одно решение, в противном случае она называется несовместной. Совместная система называется определенной, если она имеет одно решение, и неопределенной – если более одного решения. Две системы называются эквивалентными (равносильными), если множества их решений совпадают.

Ответ на вопрос о совместности системы дает теорема Кронекера-Капелли: для того чтобы система (13.7) была совместной, необходимо и достаточно, чтобы

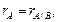
где 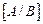– расширенная матрица системы (13.7), т. е. матрица А системы, к которой добавлен столбец B свободных членов.

Рассмотрим систему 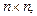имеющую вид:

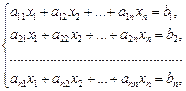(13.9)

или в матричном виде

АХ = В,

где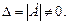

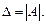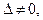Определителем системы (13.9) называется определитель матрицы этой системы (т. е. состоящий из коэффициентов системы): Если то система называется невырожденной; если 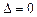– вырожденной.

Методы решения невырожденных систем используются для решения линейных систем (13.9), состоящих из n уравнений с n неизвестными, для которых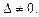

Метод обратной матрицы состоит в решении матричного уравнения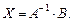

Метод Крамера также используют для решения невырожденных систем. Неизвестные находят по формулам Крамера

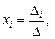
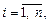(13.10)

где D _i – определитель, получаемый из определителя D системы (13.8) заменой i -го столбца столбцом свободных членов.

Решение произвольной линейной системы из m уравнений и n неизвестных начинается с нахождения ранга. Пусть 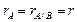и система (13.7) сведена к эквивалентной системе

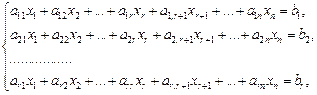(13.11)

Если 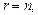то система (13.11) имеет единственное решение, которое можно получить указанными выше методами; если 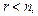то существует бесконечное множество решений. Для его получения неизвестные x ₁, x ₂, …, x_r называют базисными, x_{r + 1}, x_{r + 2}, …, x_n – свободными, система (13.11) записывается в виде

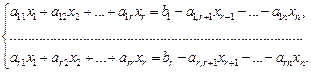
Свободным переменным присваиваются произвольные численные значения с ₁, с ₂, …, с_{n – r}.

Последняя система решается, например, методом Крамера.

Метод Гаусса используют для решения произвольных систем. С помощью элементарных преобразований над строками расширенную матрицу системы (13.7) приводят к виду

Соответствующая ей система, равносильная (13.7), примет вид:

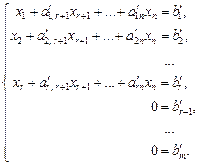(13.12)

Если хотя бы одно из чисел 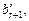…, 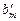отлично от нуля, то система (13.12), а значит, и исходная система (13.7) не совместны.

Если 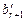= … = = 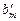0, то система (13.12) позволяет получить явное выражение для базисных неизвестных x ₁, …, x_r через свободные неизвестные x_{r +1}, …, x_n. Таким образом получают бесконечное множество решений.

Если r = n, то свободные переменные отсутствуют, а значит, системы (13.12) и (13.7) имеют единственное решение.

На практике обычно обходятся приведением матрицы системы (13.7) к треугольной или трапециевидной форме, после чего значения базисных переменных ищутся в обратном порядке.

Решение произвольной линейной системы (13.7) из m уравнений и n неизвестных целесообразно начинать с нахождения ранга. Пусть 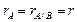и система (13.7) сведена к эквивалентной системе.

Если r = n, то система (13.7) имеет единственное решение, которое можно получить указанными выше методами. Если r < n, то существует бесконечное множество решений. Для его получения неизвестные х ₁, х ₂, …, х_r объявляют базисными, x_{r +1}, x_{r +2}, …, x_n – свободными, систему (13.12) записывают в виде

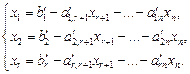
Присваивая x_{r +1}, x_{r +2}, …, x_n произвольные численные значения с ₁, с ₂, …, с_{n – r} соответственно, получают решение в виде

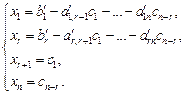
Пример 1. Решить разными способами систему уравнений

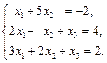
Решение. 1-й способ. Используем метод обратной матрицы. Запишем матрицу системы:

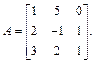
Матрица А невырожденная, так как ее определитель не равен нулю. Действительно,

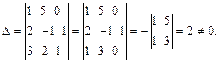(13.13)

Найдем обратную матрицу А ^–1:

А ₁₁ = –3; А ₂₁ = –5; А ₃₁ = 5;

А ₁₂ = 1; А ₂₂ = 1; А ₃₂ = –1;

А ₁₃ = 7; А ₂₃ = 13; А ₃₃ = –11.

Следовательно,

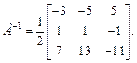
Используем далее формулу (13.10):

т. е. x ₁ = –2, x ₂ = 0, x ₃ = 8 – единственное решение.

Получаем ответ: (–2; 0; 8).

2-й способ. Используя формулы Крамера (13.10), вычисляем определитель системы (13.13).

Заменяем в определителе D первый столбец столбцом свободных членов и вычисляем

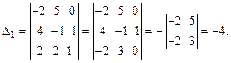
Заменяем в определителе D второй столбец столбцом свободных членов и вычисляем

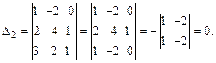
Заменяем в определителе D третий столбец столбцом свободных членов. Тогда

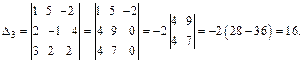
Тогда, используя формулы (13.10), получим:

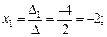
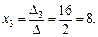
Таким образом получаем решение (–2; 0; 8).

3-й способ. Используем метод Гаусса. Приведем заданную систему к равносильной. Для этого осуществим элементарные преобразования строк расширенной матрицы системы:

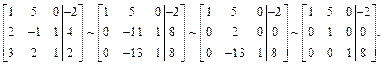
Последней матрице соответствует система

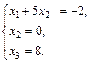
Из нее последовательно находим неизвестные, начиная с x ₃:

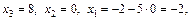
Таким образом, приходим к ответу (–2; 0; 8).

Пример 2. Исследовать систему на совместность и найти ее решение

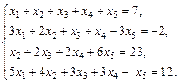
Решение. Запишем расширенную матрицу системы:

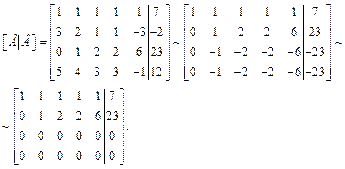
Наибольший порядок отличных от нуля миноров равен 2 (так как любой минор 3-го порядка содержит нулевую строку, то он будет равен нулю). Значит, 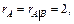т. е. исходная система совместна.

Поскольку ранг меньше количества неизвестных (2 < 5), то система имеет бесконечное множество решений.

Выберем в качестве базисного минор Тогда х ₁, х ₂ – базисные неизвестные, х ₃, х ₄, х ₅ – свободные. Система, равносильная исходной, имеет вид:

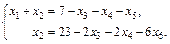
Полагаем х ₃ = с ₁, х ₄ = с ₂, х ₅ = с ₃,

где с ₁, с ₂, с ₃ – произвольные постоянные, и решаем указанную систему.

Получаем:

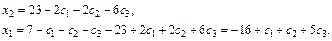
Таким образом, решение примет вид:

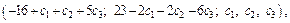
где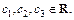

Пример 3. Найти матрицу и действительное число l, для которых выполняется условие

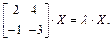
Решение. Введем обозначение 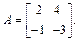Тогда условие задачи запишется в виде

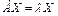или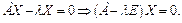

Очевидно, что при любом действительном l нулевая матрица удовлетворяет равенству, т. е. Х = 0.

Пусть 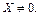Тогда ненулевое решение найдем, если матрица 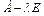окажется вырожденной, т. е. 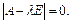Решаем последнее уравнение относительно l:

Значит, 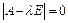при 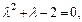что справедливо при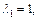

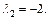
Рассмотрим случай, когда l = 1. Тогда 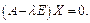Запишем последнее равенство в виде системы

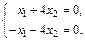
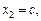Получаем Если то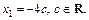

Значит, матрица X, удовлетворяющая заданному матричному уравнению при l = 1, примет вид:

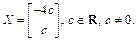
При l = –2 аналогично получим систему

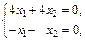
из которой находим

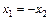или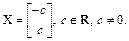

Таким образом, приходим к следующему заключению относительно выполнимости условия:

1) если l = R, то Х = 0;

2) если l = 1, то

3) если l = –2, то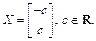

Следовательно, данная задача имеет нетривиальное (т. е. ненулевое) решение лишь при l = 1 или l = –2.

Задания

Дата добавления: 2014-01-06