Системы координат

Цилиндрическая и сферическая

Цилиндрические координаты являются обобщением полярных на случай трехмерного пространства.

Рассматривается координатная плоскость xOy с полюсом O и полярной осью Ox. Пусть M – произвольная точка пространства, а M ₁ – ее проекция на плоскость xOy. Цилиндрическими координатами точки M называются три числа 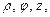где 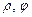– полярные координаты точки M ₁, 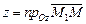(рис. 14.4), 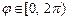или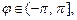

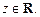
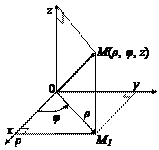
Рис. 14.4

Прямоугольные координаты x, y, z точки M будут связаны с цилиндрическими формулами:

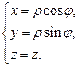(14.12)

Сферическими координатами точки M называются три числа 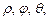где 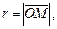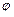– полярный угол точки M ₁, а 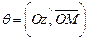(рис. 14.5),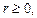 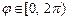или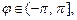

Рис. 14.5

Прямоугольные координаты точки M связывают со сферическими формулами:

(14.13)

Пример 1. Найти цилиндрические координаты по их прямоугольным координатам, если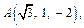

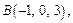
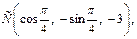
Решение. Используем рис. 14.4. Исходя из определения цилиндрических координат, имеем:

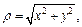
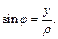
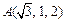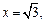
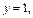
Точка имеет координаты Значит, Для нахождения удобно использовать 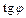с учетом четверти, в которой находится проекция A ₁ точки A на плоскость xOy (рис. 14.6), а именно: I четверти, значит,

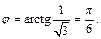
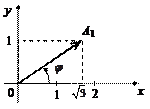
Рис. 14.6

Осталось добавить Таким образом, в цилиндрической системе координат .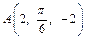

Рассмотрим точку 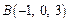. Для наглядности изобразим ее проекцию B ₁ на плоскость xOy (рис. 14.7).

Рис. 14.7

Очевидно, что 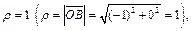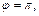остается добавить 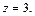Таким образом, в цилиндрической системе координат

Точка 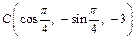имеет в плоскости xOy проекцию 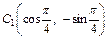(рис. 14.8), для которой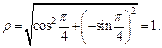

Находим полярный угол

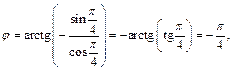
так как 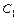находится в IV четверти (рис. 14.8).

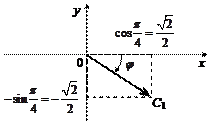
Рис. 14.8

Таким образом, в цилиндрической системе координат получаем

Точка имеет проекцией на плоскость xOy точку 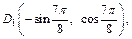находящуюся в III четверти (рис. 14.9).

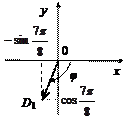
Рис. 14.9

Так как 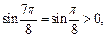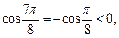причем

Для нее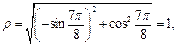

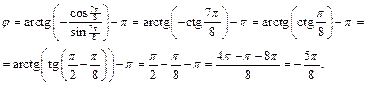
Итак,

Пример 2. Найти сферические координаты точек A (1, 1, 1), B (–4, 8, –1), C (–1, –2, –2) и D (–9, 0, 0).

Решение. Используем рис. 14.5. Сферические координаты точки M (x, y, z) выражаются через декартовы следующим образом:

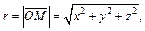
φ – полярный угол проекции точки M на плоскости xOy. 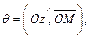что позволит для его нахождения использовать формулу

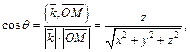
где – единичный вектор оси Oz.

Рассмотрим точку A (1, 1, 1) и ее проекцию A ₁(1, 1) на плоскость xOy (рис. 14.10).

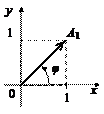
Рис. 14.10

Для них 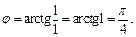поскольку 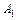лежит в I четверти, то 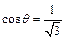или 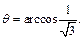Таким образом, в сферической системе координат точка .

Для точки B (–4, 8, –1) имеем 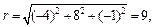проек­ция B ₁(–4, 8) на плоскость xOy определяется полярным углом (рис. 14.11).

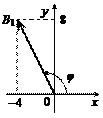
Рис. 14.11

Получаем 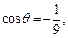откуда 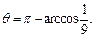Таким образом, в сферической системе координат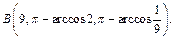

Прямоугольные координаты точки C (–1, –2, –2) и ее проекции C ₁(–1, –2) на плоскость xOy (рис. 14.12) позволяют найти сферические координаты точки C:

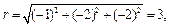
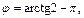
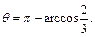
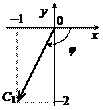
Рис. 14.12

Таким образом, в сферической системе координат

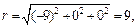
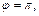
Точка D (–9, 0, 0) и ее проекция D ₁(–9, 0) на плоскость xOy приводят к сферическим координатам 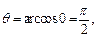т. е. в сферической системе координат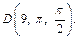

Пример 3. Найти прямоугольные координаты точек A и B, если цилиндрические координаты точки а сферические координаты точки

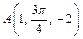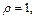
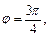
Решение. Поскольку точка задана в цилиндрической системе координат, т. е. 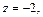то прямоугольные координаты находим по формулам (14.12):

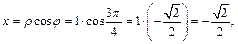
Итак, в прямоугольной декартовой системе координат .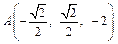

Точка 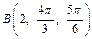задана в сферической системе координат, что значит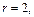 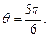Для нахождения прямоугольных координат используем формулы (14.13):

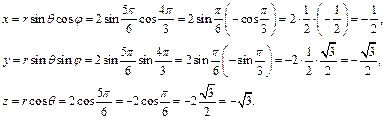
Таким образом, в прямоугольной системе координат

.

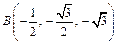Пример 4. Определить фигуры, заданные в цилиндрической системе координат соотношениями:

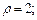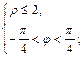1) 2) 3)

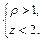
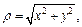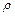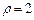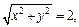
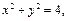
Решение. 1) Для цилиндрической системы координат где x, y – декартовы координаты проекции (при переменном значении ). Условие означает, что если 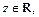значит задан круговой цилиндр.

2) Условие 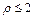в декартовых координатах означает 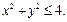Последнее условие определяет в пространстве внутреннюю область цилиндра с его границей – круговой цилиндрической поверхностью.

Уравнения и 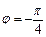задают полуплоскости, которые образуют двугранный угол. Условие 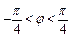означает внутреннюю область двугранного угла. Система неравенств определяет пересечение внутренней области двугранного угла и замкнутой внутренней области цилиндра.

3) Заданное условие в декартовых координатах имеет вид:

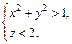
Условие задает пересечение двух открытых полупространств. Одно представляет внешнюю область кругового цилиндра 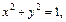а второе – часть пространства, ограниченного сверху плоскостью

Пример 5. Фигуры заданы в прямоугольных координатах. Найти уравнения этих фигур в соответствующих цилиндрических координатах:

1) 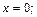2)

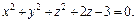
Решение. 1) Условие 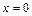в пространстве определяет координатную плоскость yOz. Используя первую формулу из (14.12), имеем 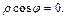Получили уравнение координатной плоскости yOz в цилиндрических координатах.

2) Выделяя полный квадрат относительно z, приходим к уравнению 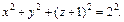Оно задает в пространстве сферу с центром (0, 0, – 1) и радиусом 2.

Пример 6. В прямоугольных координатах известны уравнения фигур:

1) 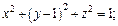2)

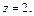
Написать эти уравнения в сферических координатах.

Решение. 1) Запишем уравнение 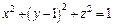в виде 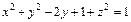или 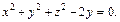Тогда, учитывая, что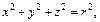 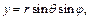имеем:

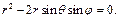
2) Поскольку то уравнение 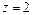примет вид: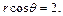

Задания

Дата добавления: 2014-01-06