Многих переменных

Основные понятия теории функций

Функции многих переменных

Пусть задано множество точек координатной плоскости Если каждой упорядоченной паре действительных чисел ставится в соответствие единственное действительное число z, то говорят, что на множестве D задана функция двух переменных со значениями в R и пишут:

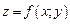или

где

Множество D называется областью определения функции f. Множество состоящее из всех чисел z, равных где называется множеством значений функции.

Множество называется открытым, если каждая точка множества принадлежит ему вместе с некоторой окрестностью этой точки. Множество называется связным, если любые две точки этого множества можно соединить непрерывной кривой, целиком принадлежащей этому множеству.

Множество, обладающее свойствами открытости и связности, называется областью.

Точка M называется граничной точкой области D, если в любой ее окрестности содержатся точки как принадлежащие D, так и не принадлежащие D.

Совокупность всех граничных точек области называется границей этой области.

Замкнутой областью называется объединение области и ее границы.

Область называется ограниченной, если все ее точки содержатся в некотором круге конечного радиуса с центром в начале системы координат.

Область называется односвязной, если для любой замкнутой кривой, принадлежащей этой области, ограниченная ею часть плоскости целиком принадлежит области D. В противном случае – область многосвязная. Многосвязная область называется n-связной, если ее граница состоит из n замкнутых кривых.

Графиком функции 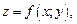определенной на области D, называется множество точек пространства R ³, где и

Множество точек для которых 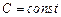(т. е. функция имеет постоянное значение С), называется линией уровня функции

С помощью линий уровня изучают вид графика функции двух переменных.

Пусть D – множество точек пространства R ³. Если каждой точке поставлено в соответствие единственное число то говорят, что на множестве D задана функция трех переменных и пишут:

или

где

Графиком функции определенной области D называется множество точек пространства R ⁴, где

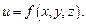
Поверхностью уровня функции трех переменных называется множество точек таких, что

Понятие функции нескольких переменных обобщается на любое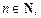

С помощью поверхностей уровня изучают вид графика функции трех переменных.

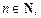
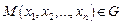Пусть G – множество точек пространства Rⁿ, Если каждой точке поставлено в соответствие единственное число то говорят, что на множестве G определена функция n переменных и пишут:

График функции переменных находится в пространстве Его невозможно изобразить геометрически для

Для функции нескольких переменных можно определить понятие предела и непрерывности. Приведем эти понятия для функции двух переменных.

Пусть некоторая точка области Множество точек для которых выполняется неравенство

называется d-окрестностью точки М ₀.

Число А называется пределом функции в точке М ₀ (при ), если такое, что для любой точки удовлетворяющей условию 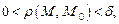выполняется неравенство

Обозначают:

или

Функция называется непрерывной в точке если

или

Функция f называется непрерывной в области D, если она непрерывна в каждой точке этой области.

Аналогичным образом определяются понятия предела и непрерывности в точке для функции n переменных,

Задания

Дата добавления: 2014-01-06