Высших порядков

Частные производные и дифференциалы

Частными производными второго порядка функции 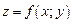называются частные производные от ее частных производных первого порядка:

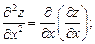(18.21)

(18.22)

(18.23)

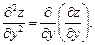(18.24)

Частные производные (18.21–18.24) обозначают также (соответственно)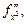

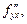
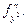
Аналогично определяются частные производные третьего, четвертого и высших порядков.

В частности,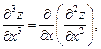

Подобным образом определяются производные высшего порядка функции трех и более переменных.

Частная производная второго порядка и выше, взятая по различным переменным, называется смешаннойчастнойпроизводной.

Если частные производные высшего порядка непрерывны, то смешанные производные одного порядка не зависят от порядка дифференцирования, например,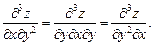

Дифференциал второго порядка функции 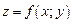определяется формулой

(18.25)

Аналогично определяются дифференциалы третьего и высших порядков.

Справедлива формула

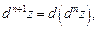
(18.26)

Если функция 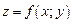имеет непрерывные частные производные, и переменные х и у являются независимыми, то дифференциалы второго и третьего порядков вычисляются по формулам:

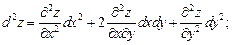(18.27)

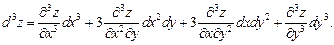(18.28)

Для всякого 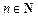формула вычисления дифференциала порядка по форме записи аналогична формуле бинома Ньютона:

(18.29)

Задания

Дата добавления: 2014-01-06