Образование проекций. Методы проецирования

Плоский чертеж какого-либо технического объекта может состо­ять из нескольких изображений, по которым и создается представле­ние об объемных формах геометрического тела. Такие плоские изо­бражения называются проекциями рассматриваемого объекта.

Под проекцией любой точки понимают ее как бы «теневое» ото­бражение на какой-либо плоскости. Так, если поместить материаль­ную точку 1 между источниками света (световых лучей) 2 и какой-либо плоскостью 3 (рисунок 2.1), то на этой плоскости увидим тень 4 этой точки, которую и принято называть проекцией точки.

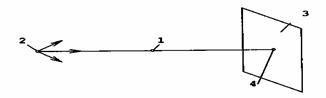
Рисунок 2.1

Взаимное положение источника света и плоскости может быть произвольным. В зависимости от величины угла между лучом 2-1-4 и плоскостью 3 возможны два принципиально отличных варианта про­екций точки:

·значение угла не равно 90°, тогда проекция точки называется ко­соугольной;

·значение угла равно 90° (прямой угол), тогда проекция называет­ся прямоугольной, или ортогональной (от греч. orthogonios - прямо­ угольный).

Курс начертательной геометрии рассматривает два основных ме­тода проецирования: центральный и параллельный.

2.1 Метод центрального проецирования

Суть метода заключается в следующем: пусть даны в пространст­ве треугольник ABC, плоскость П' и произвольная точка S (рисунок 2.2). Проведя из точки S прямые линии (лучи) через вершины треугольни­ка ABC до пересечения их с плоскостью П', получают точки А', В', С'. Эти точки называют центральными проекциями точек А, В, С. Со­единив прямыми линиями точки А', В', С', получают центральную проекцию треугольника ABC.

Точка S называется центром проецирования, плоскость П' - плос­костью проекций, прямые SA', SB', SC' - проецирующими лучами. Плоскость проекций может быть расположена и за объектом проецирования АВС как показано на рисунке 2.3.

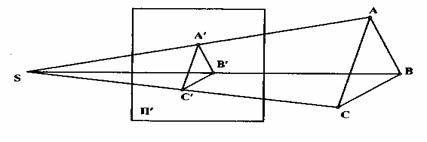
Рисунок 2.2

2.2 Метод параллельного проецирования

Если точку S удалить от плоскости П' в бесконечность, проеци­рующие лучи будут практически параллельны между собой. Тогда они пересекутся с плоскостью проекций П' в точках А', В', С', кото­рые называются параллельными проекциями точек А, В, С. Соединив, как и в предшествующем случае, точки А', В', С' между собой, полу­чают треугольник А'В'С', который будет уже параллельной проекци­ей треугольника ABC. На рисунке 2.3 стрелкой s обозначено направление проецирования.

Если направление s перпендикулярно к плоскости П', то проекция треугольника называется прямоугольной, или ортогональной.

Если направление луча s не перпендикулярно к плоскости П', то проекция треугольника называется косоугольной.

Рисунок 2.3

2.3 Система плоскостей проекций в практике решения инженерных задач

Наибольшее практическое применение нашёл метод ортогональ­ного проецирования на две взаимно перпендикулярные плоскости проекций, одна из которых расположена горизонтально, а другая - вертикально. Они соответственно получили обозначения: горизон­тальная плоскость проекций – П₁, и фронтальная — П₂. Эти плоско­сти пересекаются между собой под прямым углом, образуя линию пе­ресечения — ось х, и делят пространство на четыре четверти, которые принято обозначать против хода часовой стрелки римскими цифрами I, II, III и IV (рисунок 2.4). В случае недостаточной информативности об объекте по двум проекциям на указанные плоскости П₁ и П₂ исполь­зуют третью плоскость П₃, перпендикулярную одновременно П₁ и П₂. Она называется профильной плоскостью проекций. Плоскость Пзпе­ресекается с плоскостью П₁образуя ось у, и с плоскостью П₂, образуя ось z. Указанные плоскости делят всё пространство вокруг уже на во­семь частей, которые называются октантами и обозначаются римски­ми цифрами от I до VIII.

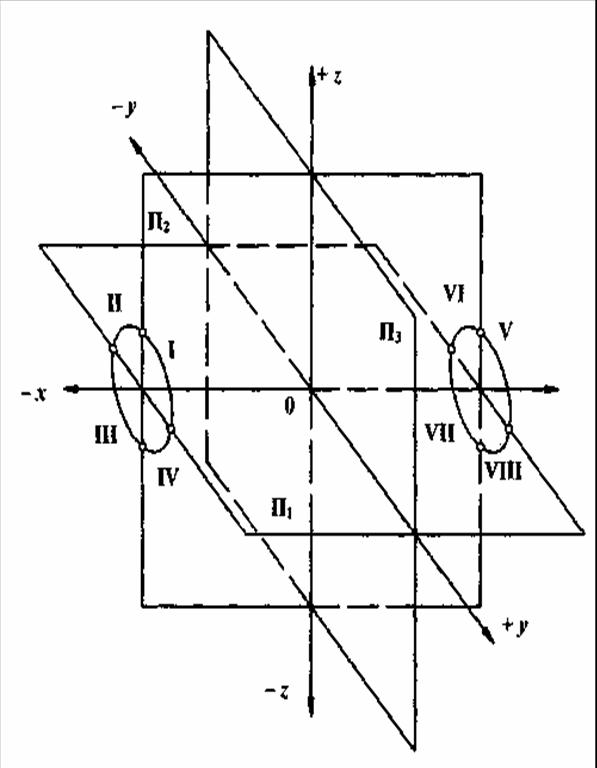
Рисунок 2.4

Дата добавления: 2014-01-06