
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 7. Оптимизация статически неопределимых систем
|
|
|
|
Оптимизация статически неопределимых систем
Основные параметры оптимизации:
- стоимость
- расход конструкционных материалов
- сроки возведения
Займемся вопросом о расходе материала
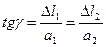 (2)
(2)
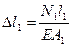 ,
,  (3)
(3)
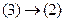 :
: 
 (**)
(**)
Обеспечиваем равнопрочность стержней 1 и 2
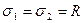 (*)
(*)
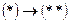 :
: 
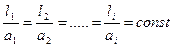 (1)
(1)
Полученное равенство дает возможность сформулировать условие равнопрочности для статически неопределимых систем: В равнопрочных стержневых системах отношение длины вертикальной подвески к ее расстоянию от шарнирно-неподвижной споры - величина постоянная.
Рассмотрим пример системы с несколькими подвесками
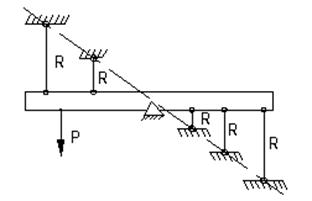
Предположим, что система будет равнопрочной, т.е. соблюдается условие 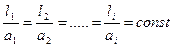
Выясним вопрос о возможности повышения несущей способности системы.
Предположим, что:
в первом стрежне площадь поперечного сечения А1 , а 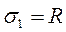 , тогда
, тогда  ;
;
во втором стержне площадь поперечного сечения А2 , а 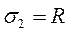 , тогда
, тогда 
Получим:  .
.
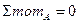 :
: 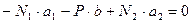

а1нов=2а 1; а2нов=2а2
Pнов= 2P, что дает возможность сделать важный вывод:
При пропорциональном увеличении расстояний от стержней подвески до опоры пропорционально растет несущая способность системы.
При увеличении плеча одного из стержней несущая способность также возрастает.
Расход материала определяется:
V= A* l
Если стержень с постоянными A и l перемещать вдоль абсолютно жесткого бруса, то объем остается постоянным. Следует добиваться наибольшего плеча силы Pотносительно шарнирно-неподвижной опоры А.
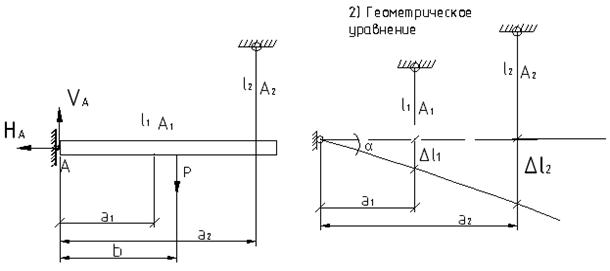
Задача:
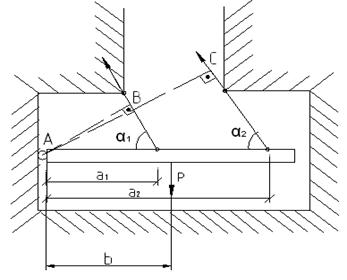
1) AB = a1*sinα
AC = a2*sinα
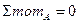
0 = N1*AB+N2*Al-Pb (І)
2) Геометрическая сторона задачи:

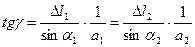 (І І)
(І І)
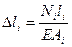 (І І І)
(І І І)

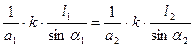
a1*sinα1 = AB = ρ1
a2*sinα2 = AB = ρ2
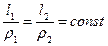 , где ρ – плечо относительно шарнирно-неподвижной опоры.
, где ρ – плечо относительно шарнирно-неподвижной опоры.
Полученное равенство дает возможность сформулировать условие равнопрочности для статически неопределимых систем с произвольным углом ориентирования повесок:
В равнопрочной статически неопределенной системе отношение длины конкретного стержня к плечу усилия в нем относительно шарнирно-неподвижной опоры – величина постоянная.
Лекция 8
Геометрические характеристики плоских сечений
Первой геометрической характеристикой является площадь поперечных сечений А (м2). Для вычисления площади необходимо:
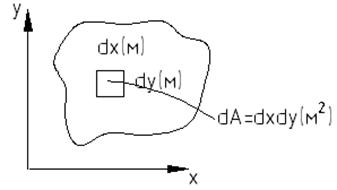
 (1) Сложные фигуры можно представить в виде набора треугольников:
(1) Сложные фигуры можно представить в виде набора треугольников:
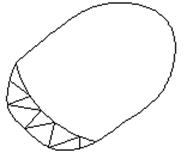
Рассмотрим вопрос о площадях и положения центра тяжести элементарных фигур.

Кроме площади поперечного сечения существует еще ряд геометрических характеристик, входящих в подавляющее число расчетных формул сопротивления материалов, напроимер:
 ,
, 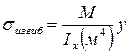
 - осевой момент инерции сечения
- осевой момент инерции сечения
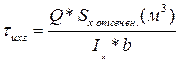
Рассмотрим статические моменты площади сечения А (м2)
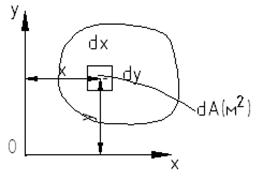
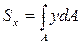 -статический момент площади относительно х (2)
-статический момент площади относительно х (2)
 -статический момент площади относительно оси y. (2.1)
-статический момент площади относительно оси y. (2.1)
Рассмотрим пример вычисления величины статического момента 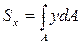 для прямоугольного поперечного сечения с габаритами b(ширина) и h(высота).
для прямоугольного поперечного сечения с габаритами b(ширина) и h(высота).
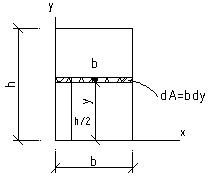
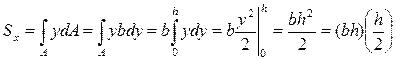
 (*),
(*),
 (3.1)
(3.1)
 (3.2)
(3.2)
По известному свойству определённого интеграла


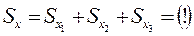 - если составляющие сложной фигуры элементарны, то можно воспользоваться формулой (*), например
- если составляющие сложной фигуры элементарны, то можно воспользоваться формулой (*), например
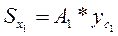
Рассмотрим пример:
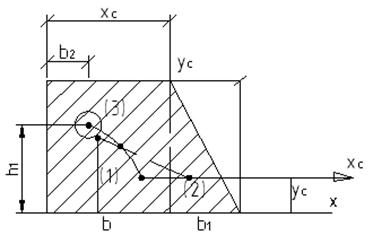
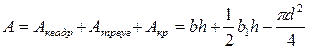


(1)
Общий алгоритм поиска координат центра тяжести сложной фигуры включает в себя следующие пункты:
- выбираем удобную для данной задачи систему координат XOY
- разбиваем сложную фигуру на элементарные составляющие
- определяем для каждого элемента фигуры ее площадь Aiи расстояние от ее центра тяжести до осей Xи Y; Xi, Yi
-подсчитвыаем величины статических моментов
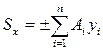 ,
, 

-  ,
, 
- откладывая отрезки xcи ycи проводя соответствие оси, определяем координаты центра точки сложной фигуры.
Моменты инерции поперечных сечений

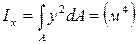 - осевой момент инерции сечения относительно OX (4.1)
- осевой момент инерции сечения относительно OX (4.1)
 -осевой момент инерции сечения относительно OY (4.2)
-осевой момент инерции сечения относительно OY (4.2)
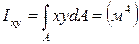 -центробежный момент инерции (4.3)
-центробежный момент инерции (4.3)
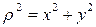
 - полярный момент инерции (4.4)
- полярный момент инерции (4.4)
Вычислим величину момента инерции для прямоугольного поперечного сечения:


Вычислим IXcотносительно оси, проходящей через центр тяжести сечения:

Момент инерции сечения относительно центральной оси меньше величин моментов инерции относительно любых других параллельных осей.
Сводка формул для величин моментов инерции элементарных фигур.

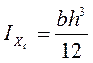
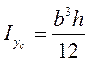


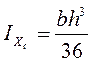

Прокатные профили:
- двутавр
- швеллер
- уголок: равнобокий, неравнобокий
- лист
- z-образный профиль
- широкополочный двутавр и т.д.
На каждый прокатный профиль существует ГОСТ.
На каждый тип профиля существует сортамент.
1) Двутавр

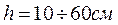
ГОСТ дает: h,b,d,A,вес 1 погонного метра, Ix, Sx, ix, Iy, Sy, iy.
Таблица сортаментов позволяет выбрать требуемый № профиля двутавра.
2) Швеллер 

В дополнение к величинам у двутавра, здесь дополнительно задается величина Z0- расстояние от наружной поверхности стенки до центра тяжести швеллера.
Уголок равнобокий

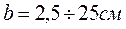
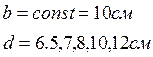 - различные толщины стенки при постоянном габарите уголка
- различные толщины стенки при постоянном габарите уголка
3) Уголок неравнобокий

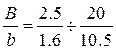
Лекция 9
В практике проектирования необходимо вычислять положение центра тяжести сложного поперечного сечения и моменты инерции сечения относительно центральной оси сечения.
У каждой фигуры есть свои собственные оси, от которых необходимо перейти к общим осям.
Рассмотрим формулы для моментов инерции сечения при параллельном переносе осей.

Формула для момента инерции относительно оси Х1:
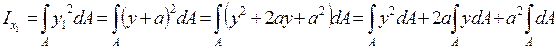
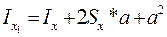

В частном случае второе слагаемое в формуле обратится в ноль - Sx=0: yc=0- ось Х проходит через центр тяжести сечения и является осью симметрии.

Xи Y– центральные оси частной фигуры.
X1и Y1- центральные оси всей фигуры.
 (1,1)
(1,1)
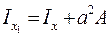 (1,2)
(1,2)
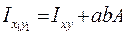 (1,3)
(1,3)
В практике проектирования встречаются следующие задачи:
При заданном расходе материала обеспечить требуемые геометрические характеристики поперечного сечения.
Здесь решается задача рационального проектирования.
2-я возможная задача: обеспечивает требуемые геометрические характеристики сечения при минимальном расходе материала (задача оптимизации). При этом возникает потребность записи величин моментов инерции при повороте осей на некоторый угол α.

 (2.1)
(2.1)
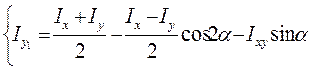 (2.2)
(2.2)
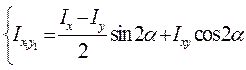 (2.3)
(2.3)
Ставим задачу поиска такого 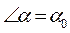 , при котором
, при котором
 ,
, 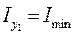 ,
, 
Используем уравнение (2.3) и получаем:
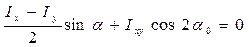 ,
, 


 ,
, 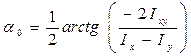 (2.4)
(2.4)
Рассмотрим сечение, у которого 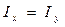

Если 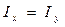 , тогда:
, тогда: 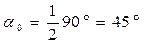
Величина угла α0 во всех случаях, когда 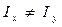 подсчитывается по формуле (2.4)
подсчитывается по формуле (2.4)
При повороте на данный угол один из моментов инерции становится максимальным, а другой минимальным.
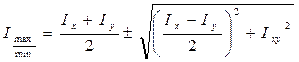 (5)
(5)

 (6)
(6)
При этом ось x1 перпендикулярна оси y1.
Сумма двух осевых моментов инерции относительно ортогональных осей – величина постоянная
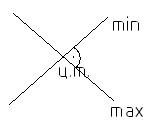
В современных расчетах случается следующие варианты:
1) За строго ограниченное время необходимо сравнивать несколько проектных решений и выбрать оптимальное
2) Обеспечить минимальный расход материалов при соблюдении всех необходимых требований к проекту
Для решения этих задач существуют современные методики вычисления геометрических характеристик плоских сечений.
Использование векторной алгебры для подсчетов величин геометрических характеристик плоских сечений

Выбираем удобную систему координат XOY
Проводим в каждой точке излома контур R-вектор из начала координат.

Вектор 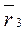 полностью определяется числами х3 и у3
полностью определяется числами х3 и у3
ДлязаданияІ:
FOR І:=1 to 15 READLN (x(І); y(І));
После ввода координат всех точек излома контура информация полностью введена.
Далее ПЭВМ считает по программе с использованием формул векторной алгебры:
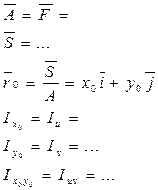
Далее ПЭВМ вычитает величины, указанные в формуле (4), и величины:

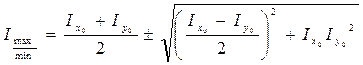
С использованием данной методики могли быть решены реальные задачи проектирования мостов и тоннелей.
Рассмотрим поперечное сечение подводного тоннеля

Ширина разреза может быть назначена в зависимости от точности масштаба.
Если встречные потоки разделены, то тоннель может иметь следующую конфигурацию.
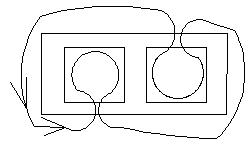
В современных условиях эксплуатации на материал конструкций действуют агрессивные среды. Рассмотрим использование программного обеспечения ПЭВМ для учета возникновения и развития коррозии на элементах сечений.
Для каждого района задается величина скорости коррозии 
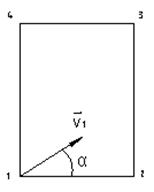
В результате можно поставить следующую задачу во времени t:
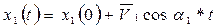
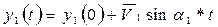
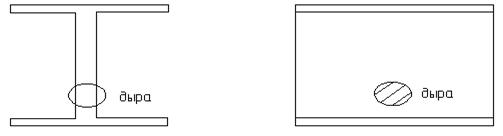
Обычно в условиях действия агрессивной среды происходит отслоение защитного слоя бетона и коррозия арматуры.
Можно подсчитать время надежной эксплуатации конструкции.
Рассмотрим двутавровое поперечное сечение.
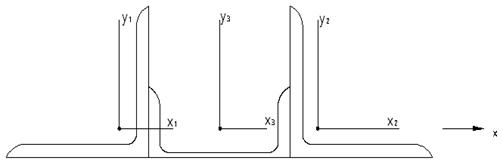
Приводим для него относительные скорости распределения коррозии по элементам сечения.

Эпюра коэффициентов скоростей коррозии по элементам профиля
Поперечное сечение должно быть проверено на момент времени t=t1,t2 с целью проверки выполнения условия:
Ix(t)>Ixmin.
В стальных мостовых конструкциях коррозия недопустима, поэтому при появлении ее признаков пятно коррозии зачищается до здорового металла с помощью пескоструйного аппарата и проводится окраска поверхности защитными грунтовками и красками.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 481; Нарушение авторских прав?; Мы поможем в написании вашей работы!