Лекция 14. Определение перемещений при изгибе балки

Определение перемещений при изгибе балки

В сопротивлении материалов перемещение определяется по формуле О. Мора:

(1)

Формула Отто Мора

М(z)_i- аналитическое выражение для изгибающего момента на этом участке балки

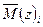- аналитическое выражение для единичного изгибающего момента на этом участке балки:

а) если требуется определить прогиб в конкретном сечении балки:

прикладываем единичную силу Р=1 в данном сечении и строим эпюру единичных моментов

б) в случае определения угла поворот в сечении прикладывается в данном сечении единичный момент m=1 и строится эпюра единичных моментов

После этого необходимо вычислить величину определенного интеграла по формуле (1).

Рассмотрим конкретный пример определения прогиба.

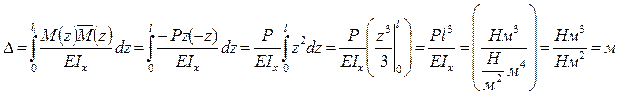
Если у балки много участков с различной нагрузкой, то вычисления по формуле (1) затруднительны.

Формула Симпсонадля определения перемещений:

(2)

Формула Симпсона дает точные величины перемещений, если эпюра М является параболой второй степени (всегда реализуется при действии равномерно распределенных нагрузок), а эпюра единичных моментов – ломаной прямой (реализуется всегда).

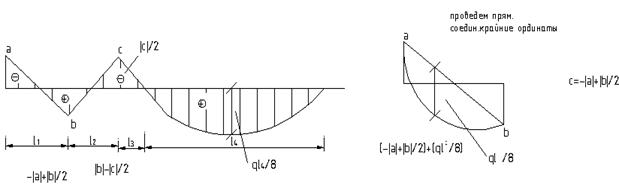
Среднее значение моментов определяется элементарно по формуле 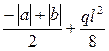(3)

(3)

Рассмотрим тот же пример, который решаем с использованием формулы Симпсона:

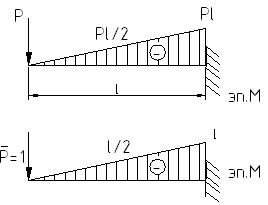
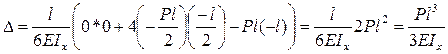- совпадает с результатом по интегралу Мора.

Рассмотрим пример определения перемещений в балке.

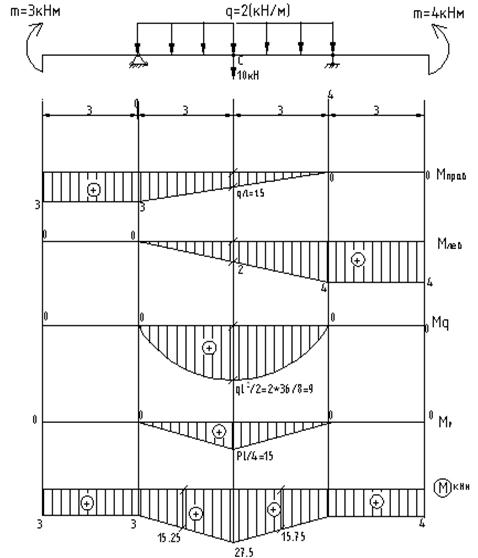
При построении эпюры изгибающих моментов используем принцип суперпозиции (эффект независимости действия си)

Эпюра единичных моментов, построенная для определения прогиба в середине балки, имеет следующий вид:

Определяем прогиб в середине балки по формуле Симпсона:

2) Рассмотрим пример определения угла поворота сечения балки

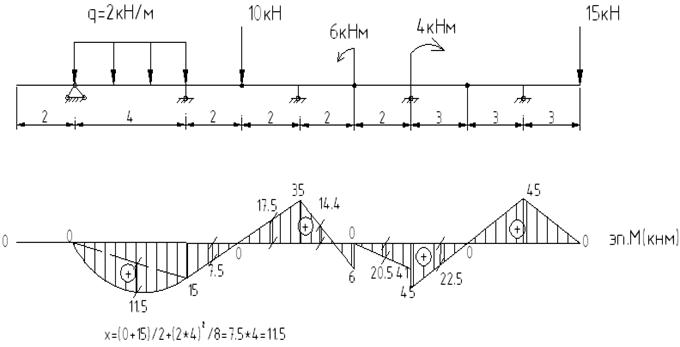
Определяем угол поворота на правой опоре балки

Угол поворота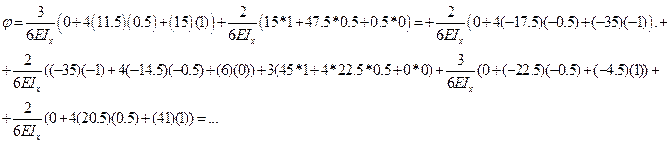

Во всех вышеприведенных вычислениях моменты записывались в (кН/м). На самом деле нужно писать в базовых единицах (Н*м), поэтому во всех вышеприведенных вычислениях умножаем полученные величины перемещений на 10³.

Рассмотрим расчет балки на жесткость (по второму предельному состоянию). Считаем, что прогиб мостовой балки не может превышать 1/450 от ее пролета. Берем конкретный пример расчета.

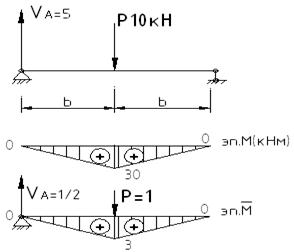
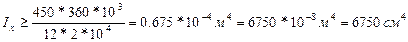
Берем I№30: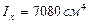

Поверим данный двутавр на прочность:

Что соответствует двутавру I№18а.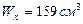

Таким образом, двутавр № 30, подобранный из условия требуемой жесткости балки, удовлетворяет и условиям прочности балки.

Дата добавления: 2014-01-06