
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 30
|
|
|
|
Расчет пластинок методом Бубнова-Галеркина.
Записываем дифференциальное уравнение изгиба элемента пластинки:
 (1)
(1)
Для конкретной задачи записывается по два граничных условия в каждой точке.

Записываем дифференциальное уравнение в безразмерном виде: при этом расчет одной пластины соответствует бесконечному множеству реальных пластин.
Вводим безразмерные переменные и функции по следующим формулам:
 ,
, 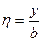

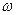 - безразмерный параметр прогиба;
- безразмерный параметр прогиба;  - толщина (м).
- толщина (м).
 ,
, 
Подставляя данные формулы в уравнение (1):
 /:
/: 

Вводим параметр 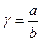


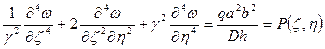 (2)
(2)
- дифференциальное уравнение изгиба пластинки в безразмерном виде.
При этом пластинка примет вид:
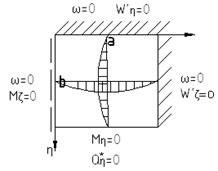
В безразмерном виде формулы для внутренних силовых факторов примут вид:
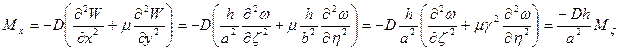
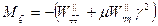 - безразмерный изгибающий момент в направлении оси ζ.
- безразмерный изгибающий момент в направлении оси ζ.
Для оси η:
 -
-
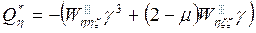
В уравнении (2) справа от знака “=”- внешние силы, а слева- внутренние.
Принцип Лагранжа: Сумма работ всех внешних и внутренних сил упругой системы на любом возможном и бесконечно малом перемещении равно 0.
Возможные перемещения должны быть совместимы с граничными условиями задач.
Применяем принцип Лагранжа к уравнению (2).
Возможное перемещение обозначим: 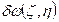 .
.
В методе Бубнова-Галеркина прогиб в первом приближении решения записаться в виде:

А- амплитуда прогиба, максимальное из решения задач по методу Бубнова-Галеркина.
Вариации прогиба записываются в виде:

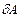 - бесконечно малое изменение амплитуды прогиба.
- бесконечно малое изменение амплитуды прогиба.
 (3)
(3)
В результате подстановки  можно записать:
можно записать:

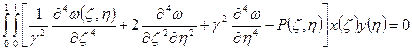
 - функция с разделяющимися переменными
- функция с разделяющимися переменными
 - функция с разделяющимися переменными
- функция с разделяющимися переменными
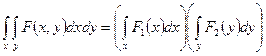
Тогда получаем следующие выражения:
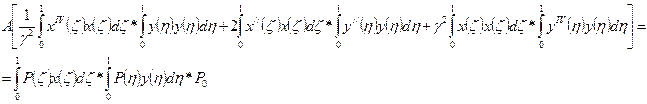
Т.к. функции 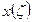 и
и  известны, то известны все величины определенных интегралов. После чего можно записать:
известны, то известны все величины определенных интегралов. После чего можно записать:

где 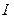 и
и  моменты инерции.
моменты инерции.
После нахождения амплитуды прогиба все величины в пластинке подсчитываются по следующим формулам:

Аналогичные формулы для этих параметров используются методом Рицце - Тимошенко.
Рассмотрим пример:


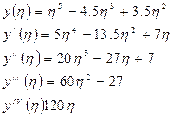
Получаем выражения для следующих производных функций

Подсчитаем интеграл: 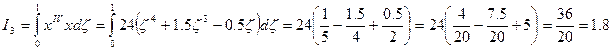

Аналогично вычисляются интегралы I1 и I4.


 в результате вычисления определенных интегралов получаются амплитуды прогибов А.
в результате вычисления определенных интегралов получаются амплитуды прогибов А.
После этого необходимо посмотреть следующие эпюры:

Чтобы не ошибиться, можно использовать ПЭВМ;
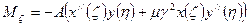
Можно записать:
WRITE (‘x=’); READLN (x);
WRITE (‘y=’); READLN (y);
WRITE (‘A=’); READLN (A);
MKS:=-A*((12*x*x-9*x)*(y*y*y+y*…)+MU*…)
WRITELN(‘MKS=’,MKS);
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 262; Нарушение авторских прав?; Мы поможем в написании вашей работы!