Lecture 1

Красса

Приложение

Замечание 11.

Замечание 10.

· В рекомендуемой литературе, в частности, в учебнике [Колемаев В.А.] приводятся таблицы для наиболее употребительных критических точек непрерывных распределений: Стьюдента: t_р= В_пa, Пирсона: c²_p=B_a, Фишера: F_р=B_a. Остальные критические точки поможет найти следующая таблица соответствий:

Критическая область	Левосторонняя	Правосторонняя	Двусторонняя
	Критическая точка	Кa	Вa	Влa	Впa
	Распределение с.в. Х
	Стъюдента, t(k)	-tр (р=2a)	tр (р=2a)	-tp (р=a)	tp (р=a)
	Пирсона, c^2(k)	c^2p (p=1-a)	c^2p (p=a)	c^2p (p=1-a/2)	c^2p (p=a/2)
	Фишера, F(k1,k2)	1/Fp (p=a)	Fp (p=a)	1/Fp (p=a/2)	Fp (p=a/2)

· Для стандартного нормального распределения двусторонние границы симметричны и имеют специальные обозначения ±u_a, т.е.B_лa=-u_a, В_пa=u_a, причем u_a является решением уравнения Ф(u_a)=(1-a)/2.

Таблица 1. Значения функции 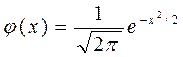(j(-х)=j(х))

	0,3989
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0	0, 2420
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0	0,0540
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3,0	0,0044
3,1
3,2
3,3
3,4
3,5
3,6
3,7
3,8
3,9

Таблица 2. Значения функции Лапласа

(Ф(-х)= -Ф(х))

х	Ф (х)	х	Ф (х)	х	Ф (х)	х	Ф(х)
0,00	0,0000	0,24	0,0948	0,48	0,1844	0,72	0,2642
0,01	0,0040	0,25	0,0987	0,49	0,1879	0,73	0,2673
0,02	0,0080	0,26	0,1026	0,50	0,1915	0,74	0,2703
0,03	0,0120	0,27	0,1064	0,51	0,1950	0,75	0,2734
0,04	0,0160	0,28	0,1103	0,52	0,1985	0,76	0,2764
0,05	0,0199	0,29	0,1141	0,53	0,2019	0,77	0,2794
0,06	0,0239	0,30	0,1179	0,54	0,2054	0,78	0,2823
0,07	0,0279	0,31	0,1217	0,55	0,2088	0,79	0,2852
0,08	0,0319	0,32	0,1255	0,56	0,2123	0,80	0,2881
0,09	0,0359	0,33	0,1293	0,57	0,2157	0,81	0,2910
0,10	0,0398	0,34	0,1331	0,58	0,2190	0,82	0,2939
0,11	0,0438	0,35	0,1368	0,59	0,2224	0,83	0,2967
0,12	0,0478	0,36	0,1406	0,60	0,2257	0,84	0,2995
0,13	0,0517	0,37	0,1443	0,61	0,2291	0,85	0,3023
0,14	0,0557	0,38	0,1480	0,62	0,2324	0,86	0,3051
0,15	0,0596	0,39	0,1517	0,63	0,2357	0,87	0,3078
0,16	0,0636	0,40	0,1554	0,64	0,2389	0,88	0,3106
0,17	0,0675	0,41	0,1591	0,65	0,2422	0,89	0,3133
0,18	0,0714	0,42	0,1628	0,66	0,2454	0,90	0,3159
0,19	0,0753	0,43	0,1664	0,67	0,2486	0,91	0,3186
0,20	0,0793	0,44	0,1700	0,68	0,2517	0,92	0,3212
0,21	0,0832	0,45	0,1736	0,69	0,2549	0,93	0,3238
0,22	0,0871	0,46	0,1772	0,70	0,2580	0,94	0,3264
0,23	0,0910	0,47	0,1808	0,71	0,2611	0,95	0,3289
0,96	0,3315	1,37	0,4147	1,78	0,4625	2,36	0,4909
0,97	0,3340	1,38	0,4162	1,79	0,4633	2,38	0,4913
0,98	0,3365	1,39	0,4177	1,80	0,4641	2,40	0,4918
0,99	0,3389	1,40	0,4192	1,81	0,4649	2,42	0,4922
1,00	0,3413	1,41	0,4207	1,82	0,4656	2,44	0,4927
1,01	0,3438	1,42	0,4222	1,83	0,4664	2,46	0,4931
1,02	0,3461	1,43	0,4236	1,84	0,4671	2,48	0,4934
1,03	0,3485	1,44	0,4251	1,85	0,4678	2,50	0,4938
1,04	0,3508	1,45	0,4265	1,86	0,4686	2,52	0,4941
1,05	0,3531	1,46	0,4279	1,87	0,4693	2,54	0,4945
1,06	0,3554	1,47	0,4292	1,88	0,4699	2,56	0,4948
1,07	0,3577	1,48	0,4306	1,89	0,4706	2,58	0,4951
1,08	0,3599	1,49	0,4319	1,90	0,4713	2,60	0,4953
1,09	0,3621	1,50	0,4332	1,91	0,4719	2,62	0,4956
1,10	0,3643	1,51	0,4345	1,92	0,4726	2,64	0,4959
1,11	0,3665	1,52	0,4357	1,93	0,4732	2,66	0,4961
1,12	0,3686	1,53	0,4370	1,94	0,4738	2,68	0,4963
1,13	0,3708	1,54	0,4382	1,95	0,4744	2,70	0,4965
1,14	0,3729	1,55	0,4394	1,96	0,4750	2,72	0,4967
1,15	0,3749	1,56	0,4406	1,97	0,4756	2,74	0,4969
1,16	0,3770	1,57	0,4418	1,98	0,4761	2,76	0,4971
1,17	0,3790	1,58	0,4429	1,99	0,4767	2,78	0,4973
1,18	0,3810	1,59	0,4441	2,00	0,4772	2,80	0,4974
1,19	0,3830	1,60	0,4452	2,02	0,4783	2,82	0,4976
1,20	0,3849	1,61	0,4463	2,04	0,4793	2,84	0,4977
1,21	0,3869	1,62	0,4474	2,06	0,4803	2,86	0,4979
1,22	0,3883	1,63	0,4484	2,08	0,4812	2,88	0,4980
1,23	0,3907	1,64	0,4495	2,10	0,4821	2,90	0,4981
1,24	0,3925	1,65	0,4505	2,12	0,4830	2,92	0,4982
1,25	0,3944	1,66	0,4515	2,14	0,4838	2,94	0,4984
1,26	0,3962	1,67	0,4525	2,16	0,4846	2,96	0,4985
1,27	0,3980	1,68	0,4535	2,18	0,4854	2,98	0,4986
1,28	0,3997	1,69	0,4545	2,20	0,4861	3,00	0,49865
1,29	0,4015	1,70	0,4554	2,22	0,4868	3,20	0,49931
1,30	0,4032	1,71	0,4564	2,24	0,4875	3,40	0,49966
1,31	0,4049	1,72	0,4573	2,26	0,4881	3,60	0,499841
1,32	0,4066	1,73	0,4582	2,28	0,4887	3,80	0,499928
1,33	0,4082	1,74	0,4591	2,30	0,4893	4,00	0,499968
1,34	0,4099	1,75	0,4599	2,32	0,4898	4,50	0,499997
1,35	0,4115	1,76	0,4608	2,34	0,4904	5,00	0,499997
1,36	0,4131	1,77	0,4616

Таблица 3. Значения функции t_g=t(g,n)

n	g	n	g
0,95	0,99	0,999	0,95	0,99	0,999
	2,78	4,60	8,61		2,093	2,861	3,883
	2,57	4,03	6,86		2,064	2,797	3,745
	2,45	3,71	5,96		2,045	2,756	3,659
	2,37	3,50	5,41		2,032	2,720	3,600
	2,31	2,36	5,04		2,023	2,708	3,558
	2,26	3,25	4,78		2,016	2,692	3,527
П	2,23	3,17	4,59		2,009	2,679	3,502
	2,20	3,11	4,44		2,001	2,662	3,464
	2,18	3,06	4,32		1,996	2,649	3,439
	2,16	3,01	4,22		1,001	2,640	3,418
	2,15	2,98	4,14		1,987	2,633	3,403
	2,13	2,95	4,07		1,984	2,627	3,392
	2,12	2,92	4,02		1,980	2,617	3,374
	2,11	2,90	3,97	¥	1,960	2,576	3,291
	2,10	2,88	3,92

Таблица 4. Значения функции q=q(g,n)

n	g	n	g
0,95	0,99	0,999	0,95	0,99	0,999
	1,37	2,67	5,64		0,37	0,58	0,88
	1,09	2,01	3,88		0,32	0,49	0,73
	0,92	1,62	2,98		0,28	0,43	0,63
	0,80	1,38	2,42		0,26	0,38	0,56
	0,71	1,20	2,06		0,24	0,35	0,50
	0,65	1,08	1,80		0,22	0,32	0,46
	0,59	0,98	1,60		0,21	0,30	0,43
	0,55	0,90	1,45		0,188	0,269	0,38
	0,52	0,83	1,33		0,174	0,245	0,34
	0,48	0,78	1,23		0,161	0,226	0,31
	0,46	0,73	1,15		0,151	0,211	0,29
	0,44	0,70	1,07		0,143	0,198	0,27
	0,42	0,66	1,01		0,115	0,160	0,211
	0,40	0,63	0,96		0,099	0,136	0,185
	0,39	0,60	0,92		0,089	0,120	0,162

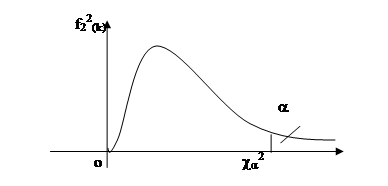
Таблица 5. Критические точки c_a² распределения c² соответствующие вероятности a=P(c²(k)> c_a²)

Число степеnей свободы к	Уровеннь значимости a
0,99	0,975	0,95	0,90	0,10	0,05	0,025	0,01
	0,0002	0,001	0,004	0,02	2,71	3,84	5,0	6,64
	0,02	0,051	0,10	0,21	4,61	5,99	7.4	9,21
	0,12	0.216	0.35	0,58	6,25	7,82	9,4	11,34
	0,30	0,484	0,71	1,06	7,78	9,49	11,1	13,28
	0,55	0,831	1,15	1,61	9,24	11,07	12,8	15,09
	0,87	1,24	1,64	2,20	10,65	12,59	14,4	16,81
	1,24	1,69	2,17	2,83	12,02	14,06	16,0	18,48
	1,65	2,18	2,73	3,49	13,36	15,51	17.5	20,09
	2,09	2.70	3,33	4,17	14,68	16,92	19,0	21,67
	2,56	3.25	3,94	4,87	15,99	18,31	20.5	23,21
	3,05	3.82	4,58	5,58	17,28	19,68	21,9	24,72
	3,57	4.40	5,23	6,30	18,55	21,03	23,3	26,22
	4,11	5,01	5,89	7,04	19,81	22,36	24,7	27,68
	4,66	5,63	6,57	7,79	21,06	23,69	26,1	29,14
	5,23	6.26	7,26	8.55	22,31	25,00	27.5	30,58
	5,81	6.91	7,96	9.31	23,54	26,30	28.8	32,00
	6,41	7,56	8,67	10,09	24,77	27,59	30,2	33,41
	7,02	8.23	9,39	10,86	25,99	28,87	31.5	34,81
	7,63	8.91	10,12	11,65	27,20	30,14	32,9	36,19
	8,26	9.59	10,85	12,44	28,41	31,41	34,2	37,57
	8,90	10.3	11,59	13,24	29,62	32,67	35.5	38,93
	9,54	11.0	12,34	14,04	30,81	33,92	36,8	40,29
	10,20	11.7	13,09	14,85	32,01	35,17	38,1	41,64
	10,86	12,4	13,85	15,66	33,19	36,42	39,4	43,98
	11,52	13,1	14,61	16,47	34,38	37,65	40,6	44,31
	12,20	13,8	15,37	17,29	35,56	38,89	41,9	45,64
	12,88	14,6	16,15	18,11	36,74	40,11	43.2	46,96
	13,56	15,3	16,93	18,94	37,92	41,34	44,5	48,28
	14,26	16,0	17,71	19,77	39,09	42,56	45.7	49,59
	14,95	16,8	18,49	20,60	40,26	43,77	47,0	50,89
	22,16		26,51	29,05	51,81	55,76		63,69
	29,71		34,76	37,69	63,17	67,51		76,15
	70,07		77,93	82,36	118,50	124,34		135,81

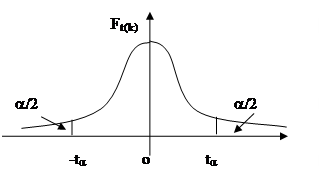
Таблица 6. Критические точки распределения Стьюдента, значения t_a, соответствующие вероятности a=P(t(k)>t_a)

Число степеней свободы к	Уровень значимости a (двусторонняя критическая область)
0,1	0,05	0,02	0,01	0,005	0,001
	6,31	12,71	31,82	63,66	127,32	637,0
	2,92	4,30	6,97	9,92	14,09	31,6
	2,35	3,18	4,54	5,84	7,45	12,9
	2,13	2,78	3,75	4,60	5,60	8,61
	2,01	2,57	3,37	4,03	4,77	6,86
	1,94	2,45	3,14	3,71	4,32	5,96
	1,89	2,36	3,00	3,50	4,03	5,40
	1,86	2,31	2,90	3,36	3,83	5,04
	1,83	2,26	2,82	3,25	3,69	4,78
	1,81	2,23	2,76	3,17	3,58	4,59
	1.80	2,20	2,72	3,11	3,50	4,44
	1,78	2,18	2,68	3,05	3,43	4,32
	1,77	2,16	2,65	3,01	3,37	4,22
	1,76	2,14	2,62	2,98	3,33	4,14
	1,75	2,13	2,60	2,95	3,29	4,07
	1,75	2,12	2,58	2,92	3,25	4,01
	1,74	2,11	2,57	2,90	3,22	3,96
	1,73	2,10	2,55	2,88	3,20	3,92
	1,73	2,09	2,54	2,86	3,17	3,88
	1,72	2,09	2,53	2,85	3,15	3,85
	1,71	2,06	2,49	2,79	3,08	3,72
	1,70	2,04	2,46	2,75	3,03	3,66
	1,68	2,02	2,42	2,70	2,97	3,55
	1,67	2,00	2,39	2,66	2,91	3,46
	1,66	1,98	2,36	2,62	2,86	3,37
¥	1,64	1,96	2,33	2,58	2,81	3,29
	0,05	0,025	0,01	0,005	0,025	0,0005
Уровень значимости a (односторонняя критическая область)		Уровень значимости a (односторонняя критическая область)

Таблица 7. Критические точки распределения F Фишера, значения F_a, соответствующие вероятности a=P(F(k₁,k₂)>F_a) при a=0,05

K2	K1
									¥
	161,45	199,50	215,71	224,58	230,16	233,99	238,88	243,91	249,05	254,32
	18,51	19,00	19,16	19,25	19,30	19,33	19,37	19,41	19,45	19,50
	10,13	9,55	9,28	9,12	9,01	8,94	8,84	8,74	8,64	8,53
	7,71	6,94	6,59	6,39	6,26	6,16	6,04	5,91	5,77	5,63
	6,61	5,79	5,41	5,19	5,05	4,95	4,82	4,68	4,53	4,36
	5,99	5,14	4,76	4,53	4,39	4,28	4,15	4,00	3,84	3,67
	5,59	4,74	4,35	4,12	3,97	3,87	3,73	3,57	3,41	3,23
	5,32	4,46	4,07	3,84	3,69	3,58	3,44	3,28	3,12	2,93
	5,12	4,26	3,86	3,63	3,48	3,37	3,23	3,07	2,90	2,71
	4,96	4,10	3,71	3,48	3,33	3,22	3,07	2,91	2,74	2,54
	4,84	3,98	3,59	3,36	3,20	3,09	2,95	2,79	2,61	2,40
	4,75	3,88	3,49	3,26	3,11	3,00	2,85	2,69	2,50	2,30
	4,67	3,80	3,41	3,18	3,02	2,92	2,77	2,60	2,42	2,21
	4,60	3,74	3,34	3,11	2,96	2,85	2,70	2,53	2,35	2,13
	4,54	3,68	3,29	3,06	2,90	2,79	2,64	2,48	2,29	2,07
	4,49	3,63	3,24	3,01	2,85	2,74	2,59	2,42	2,24	2,01
	4,45	3,59	3,20	2,96	2,81	2,70	2,55	2,38	2,19	1,96
	4,41	3,55	3,16	2,93	2,77	2,66	2,51	2,34	2,15	1,92
	4,38	3,52	3,13	2,90	2,74	2,63	2,48	2,31	2,11	1,88
	4,35	3,49	3,10	2,87	2,71	2,60	2,45	2,28	2,08	1,84
	4,24	3,38	2,99	2,76	2,60	2,49	2,34	2,16	1,96	1,71
	4,17	3,32	2,92	2,69	2,53	2,42	2,27	2,09	1,89	1,62
	4,08	3,23	2,84	2,61	2,45	2,34	2,18	2,00	1,79	1,51
	4,00	3,15	2,76	2,52	2,37	2,25	2,10	1,92	1,70	1,39
	3,92	3,07	2,68	2,45	2,29	2,17	2,02	1,83	1,61	1,25
¥	3,84	2,99	2,60	2,37	2,21	2,09	1,94	1,75	1,52	1,00

Лекции по теоретической фонетике
Примерные вопросы для контроля знаний

1. Phonetics as a branch of linguistics. Phonetics and other disciplines. Applications of phonetics.

2. Branches of phonetics.

3. Aspects of the sound matter of language.

4. Components of the phonetic system of language.

5. National and regional pronunciation variants in English.

6. British and American pronunciation models.

7. Most distinctive features of BBC English and Network English.

8. The articulatory classification of English vowels.

9. The articulatory classification of English consonants.

10. Phoneme as many-sided dialectic unity of language. Types of allophones. Distinctive and irrelevant features of the phoneme.

11. Main phonological schools.

12. The system of vowel phonemes in English. Problem of diphthongs.

13. The system of consonant phonemes in English. Problem of affricates.

14. Modifications of English consonants and vowels in speech.

15. Alternations of speech sounds in English.

16. Theories on syllable division and formation.

17. The structure and functions of syllable in English.

18. Word stress in English.

19. Intonation and prosody: definition, functions, components, spheres of application.

20. The structure of English tone-group.

21. The phonological level of intonation.

22. Methods of phonetic analysis.

23. Phonostylistics. Types and styles of pronunciation in English.

24. Phonetics of the spoken discourse.

Дата добавления: 2014-01-06