Способы записи алгоритмов

В учебниках информатики выделяют разные способы записи алгоритмов. В частности, алгоритм можно записать на обычном (естественном языке) – в этом случае говорят о словесном способе задания алгоритма. Нотную запись музыкальной мелодии допустимо рассматривать в качестве способа задания алгоритма ее исполнения (на языке музыки). На языке математики с помощью формул записываются алгоритмы вычисления различных математических величин и т. д. Выделяя графические способы задания алгоритма, упоминают о чертежах, регламентирующих процесс строительства зданий и производства деталей и т.п. При таком понимании под графический способ задания алгоритма попадает и маршрут геологической партии, нанесенный на карту, и блок-схема алгоритма.

В качестве особого способа задания алгоритмов рассматриваются компьютерные программы, кодирующие алгоритмы на формальных языках программирования.

При всех различиях в записи алгоритмов, при всем разнообразии исполнителей и задач, решаемых ими, алгоритм не отождествляется с любой последовательностью действий того или иного исполнителя. Даже на интуитивном уровне подразумевается, что последовательность действий, именуемая алгоритмом, должна обладать вполне определенными свойствами, позволяющими отличать алгоритм, от «не алгоритма».

3. Свойства алгоритмов

В общем случае полагается, что алгоритм должен обладать важнейшим качеством (свойством) – исполнение алгоритма в одних и тех же условиях различными исполнителями (людьми или устройствами) должно приводить к одинаковым результатам. Это свойство в разных источниках называется по-разному: одназначностью, определенностью.

Тот факт, что алгоритм – суть набора отдельных команд, допускающих пошаговое исполнение, характеризуется таким свойством, как дискретность.

Принципиальная достижимость результата, заключающаяся в том, что при точном исполнении команд (предписаний) алгоритма процесс должен прекратится за конечное число шагов, приводя к заданному результату, фиксируется таким свойством алгоритма, как результативность.

Еще одно свойство алгоритма характеризуется термином «понятность». В соответствие с ним алгоритм должен состоять из команд, однозначно понимаемых (исполняемых) исполнителем. Иными словами, алгоритм не должен включать команды, которые не входят в систему команд исполнителя.

Такого рода требования предопределяют возможность формального исполнения алгоритма, не предполагающего от исполнителя осмысленности выполняемых действий, а также действий, не предусмотренных алгоритмом.

4. Исполнители и алгоритмы в школьной информатике

Идея определения алгоритма как последовательности предписаний из системы команд некоторого исполнителя, восходящая, пожалуй, к работам А.Тьюринга и Э.Поста, оказалась плодотворной не только в рамках формальной теории вычислимости[2], но и в рамках теории и методики обучения информатике. Так, в учебниках «Алгоритмика» [], [] для средней школы можно найти множество Исполнителей – и простых, и сложных. Например, Исполнитель под названием Удвоитель описывается следующим образом:

«Удвоитель – это воображаемое устройство с экраном и двумя кнопками. На экране написано число. Когда мы включаем Удвоитель, это число равно 0. На кнопках написано «прибавь 1» и «умножь на 2». При нажатии на первую клавишу число, изображенное на экране, увеличивается на 1. При нажатии на вторую клавишу число на экране удваивается» [] (см. рис. 1).

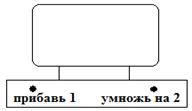
Рис. 1. Удвоитель

Несмотря на простоту Удвоителя, его можно использовать для знакомства школьников с двоичной системой счисления, с понятием эффективности программы. Получить на экране заданное число – задача простая. Но сделать это за наименьше число команд, да еще доказать, что это число наименьшее – задача сложнее.

Описание в «Алгоритмике» Директора Строительства выглядит следующим образом:

«1) Вы Директор Строительства. В вашем распоряжении несколько строительных бригад, которым вы должны давать работу.

2) Всякий кубик (блок) независимо от своего вида и размера может быть установлен одной бригадой за один день. Две бригады не могут устанавливать один и тот же блок.

3) Строительство блока может начаться только после того, как установлены все блоки, на которые он опирается» [ ].

Пример «строительного объекта» приведен на рис. 2.

Рис. 2. Строительный объект для Директора Строительства

Рассматривая каждую бригаду как отдельного исполнителя, у которого всего одна команда установи <номер>, Директор Строительства может написать следующую программу строительства объекта (на рис.2) с помощью двух бригад:

	1 бригада	2 бригада
1 день	установи (1)	установи (2)
2 день	установи (3)	установи (9)
3 день	установи (4)	установи (6)
4 день	установи (5)	установи (10)
5 день	установи (7)	установи (11)
6 день	установи (8)	установи (12)

Как представляется, решение подобных задач – неплохая пропедевтика параллельного программирования.

Впрочем, Исполнителей в школьной информатике много, что свидетельствует об их высоком дидактическом потенциале. Но мы ограничимся только приведенными примерами, поскольку далее в центре нашего внимания будут более сложные математические объекты.

Дата добавления: 2014-01-06