Характеризация праволинейных языков

Теорема 10.2.1. Каждый автоматный язык является праволинейным.

Доказательство. Пусть автоматный язык L (M) определяется конечным автоматом М=< Q, A, D, I, F >, где QÇA=Æ, и I ={ q₀ }. Положим N=Q, S=q₀, P ={ p®xq: < p, x, q >Î D }È{ p®e: p Î F }. Тогда G=< N, A, P, S > – праволинейная грамматика (грамматика типа 3), порождающая язык L (M).

Теорема доказана.

Теорема 10.2.2. Каждый праволинейный язык является автоматным.

Доказательство. Без ограничения общности можно считать, что праволинейный язык L задан праволинейной грамматикой, не содержащей правил вида T®u, где uÎA⁺. Положим:

Q=N, I= { S }, F ={ TÎN: (T®e) ÎP }, D ={< T, u, B >: (T®uB) ÎP }.

Тогда конечный автомат М=< Q, A, D, I, F > порождает такой язык L (M), что L=L (M).

Теорема доказана.

Пример 10.2.1. Праволинейный язык

L ={ w Î{ a, b } ^*: ç w ç _amod 2 =0, ç w ç _bmod 2 =0}

порождается грамматикой G=< N, A, P, S >, где N ={ S, T, E, F }, A={ a, b }, P ={ S®aT, S®bE, S®e, T®aS, T®bF, E®aF, E®bS, F®aE, F®bD }.

Диаграмма переходов конечного автомата M₃, порождающего этот же язык имеет вид:

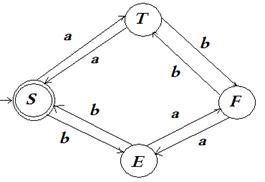
Рис. 10.2.1. Диаграмма конечного автомата М₃

Определение 10.2.1. Праволинейная грамматика, в которой каждое правило имеет вид T®e, T®a, T®aU, где T, UÎN, aÎA, называется праволинейной грамматикой в нормальной форме (автоматной грамматикой, регулярной грамматикой).

Теорема 10.2.3. Каждая праволинейная грамматика эквивалентна некоторой праволинейной грамматике в нормальной форме.

Теорема 10.2.4. Класс праволинейных языков замкнут относительно итерации, конкатенации и объединения.

Теорема 10.2.5. Класс праволинейных языков замкнут относительно дополнения и пересечения.

Теорема 10.2.6. Пусть L – праволинейный язык над алфавитом А. Тогда найдется такое натуральное p >0, что для любого слова wÎL ç w ç³ p можно подобрать слова x, y, zÎA^*, для которых справедливы соотношения :y¹e, ç xy ç£ p, xyz=w, xyⁱzÎL (для всех i ³0).

Пример 10.2.2. Пусть язык L= { abⁿaⁿ: n ³0} задан над алфавитом A={a, b}.

Пусть p – произвольное натуральное число. Положим w=ab^pa^p_.

Если положить x=e, то возможны следующие варианты:

y	Z	w	xyyz
a	b^pa^p	xyz	aab^pa^pÏL
ab^k(0<k<p)	b^p-ka^p	xyz	ab^kab^pa^pÏL
ab^p	a^p	xyz	ab^pab^pa^pÏL
ab^pa^k(0<k£p)	a^p-k	xyz	ab^pa^k+1b^pa^pÏL

Как видно из приведенной таблицы, при любом натуральном p и x=e слово xyyzÏL. С помощью а налогичных выкладок можно придти к выводу о том, что при любом натуральном p и при x=a слово xyyzÏL. Этот же вывод оказывается верен и при x=ab^k, x=ab^pa^k. В свою очередь, это означает, что условие теоремы 10.2.6 не выполняется, а потому язык L не является автоматным.

Дата добавления: 2014-01-06