Метод простой итерации

Else

E-006

0.3942

Else

x1=c;

end;

L=x2-x1;

end;

z=c;

3. Построение графика функции на интервале [-1,1]

>> x1=-1;

>> x2=1;

>> dx=10^-3;

>> x=x1:dx:x2;

>> plot(x,Func(x)); grid on

Рис. 2.2

4. Вычисление значения корня уравнения

>> Div2('Func',x1,x2,10^-5)

ans =

5. Проверка полученного значения корня

>> Func(ans)

ans =

Для рассмотрения процесса нахождения корня уравнения в динамике, необходимо сохранить значение корня на каждом шаге вычислительной процедуры и построить зависимость значения корня от номера шага. Ниже приведен листинг файла Div2I.m, содержащего описание функции, возвращающей значение корня и длины отрезка, на котором данный корень находится, на каждом шаге метода половинного деления.

% листинг файла Div2I.m

function [z1,z2]=Div2(f,x1,x2,eps);

k=1;

L(1)=x2-x1; % начальная длина отрезка

c(1)=(x2+x1)/2; % начальное значение корня

while L(k)>eps

if feval(f,c(k))*feval(f,x1)<0

x2=c(k);

x1=c(k);

end;

k=k+1;

c(k)=(x2+x1)/2;

L(k)=x2-x1;

end;

z1=c;

z2=L;

6. Вычисление значений корня и длины отрезка, на котором ищется решение, на каждом шаге итерационного процесса

>> [c L]=Div2I('Func',x1,x2,10^-5);

Рис. 2.3. Зависимость значения корня от номера шага вычислительной процедуры

5. Визуализации зависимости значения корня от номера итерационного процесса (рис. 2.3)

>> plot(c, '-o')

6. Визуализация зависимости длины отрезка, на котором ищется значение корня, от номера итерации (рис. 2.4)

>> plot(L, '-o')

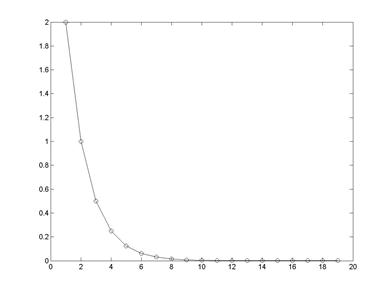
Рис. 2.4. Зависимость длины отрезка, на котором ищется значение корня, от номера шага вычислительной процедуры

Заменим уравнение (2.1) равносильным уравнением

x = f (x). (2.4)

Пусть x - корень уравнения (2.4), а x ₀, полученное каким либо способом нулевое приближение к корню x. Подставляя x ₀ в правую часть уравнения (2.4), получим некоторое число x ₁ = f (x ₀). Повторим данную процедуру с x ₁ и получим x ₂ = f (x₁). Повторяя описанную процедуру, получим последовательность

x ₀, x ₁,… x_n, …, (2.5)

называемую итерационной последовательностью.

Геометрическая интерпретация данного алгоритма представлена на рис. 2.6.

Рис. 2.6

Итерационная последовательность, вообще говоря, может быть как сходящейся, так и расходящейся, что определяется видом функции f (x).

Теорема 2.1. Если функция f (x) непрерывна, а последовательность (2.5) сходится, то предел последовательности (2.5) является корнем уравнения (2.4).

Действительно, пусть . Перейдем к пределу в равенстве :

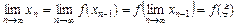. (2.6)

Условие сходимости итерационного процесса определяется теоремой о достаточном условии сходимости итерационного процесса.

Теорема 2.2. Пусть уравнение 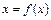имеет единственный корень на отрезке и выполнены условия:

1) 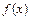определена и дифференцируема на ;

2) для всех ;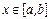

3) существует такое вещественное q, что для всех .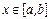

Тогда итерационная последовательность (n = 1, 2, …) сходится при любом начальном приближении .

Доказательство. Построим итерационную последовательность вида (2.5) с любым начальным значением . В силу условия 2 теоремы 2.2 все члены последовательности находятся в отрезке .

Рассмотрим два последовательных приближения и . По теореме Лагранжа о конечных приращениях имеем

.

Переходя к модулям и принимая во внимание условие 3 теоремы 2.2, получим

.

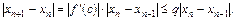
При n = 1, 2, … имеем

(2.7)

….

.

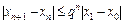Рассмотрим ряд

(2.8)

Составим частичные суммы этого ряда

.

Заметим, что (n +1)-я частичная сумма ряда (2.8) совпадает с n -ым членом итерационной последовательности (2.5), т.е.

. (2.9)

Сравним ряд (2.8) с рядом

(2.10)

Заметим, что в силу соотношения (2.7) абсолютные величины членов ряда (2.8) не превосходят соответствующих членов ряда (2.10). Но ряд (2.10) сходится как бесконечно убывающая геометрическая прогрессия (q < 1, по условию). Следовательно, и ряд (2.8) сходится, т.е. его частичная сумма (2.9) имеет предел. Пусть . В силу непрерывности функции f получаем (cм. (2.6)):

т.е. x - корень уравнения .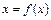

Отметим, что условия теоремы не являются необходимыми. Это означает, что итерационная последовательность может оказаться сходящейся и при невыполнении этих условий.

Найдем погрешность корня уравнения, найденного методом простой итерации. Пусть x_n - приближение к истинному значению корня уравнения x = f (x). Абсолютная ошибка приближения x_n оценивается модулем

.

Принимая во внимание (2.8) и (2.9), имеем

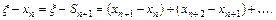(2.11)

Сравним (2.11) с остатком ряда (2.9):

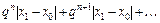(2.12)

Учитывая оценку (2.7), получаем

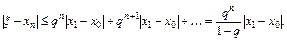
Таким образом, для оценки погрешности n -го приближения получается формула

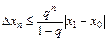. (2.13)

На практике удобнее использовать модификацию формулы (2.13).

Примем за нулевое приближение (вместо 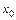). Следующим приближением будет (вместо ).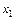

Так как , то

. (2.14)

При заданной точности ответа e итерационный процесс прекращается, если .

Дата добавления: 2014-01-06