Метод Зейделя

0.9672

2.2930

0.7787 1.0119 0.9636

0.2016 -0.3626 0

0.5131 0 -0.2656

0 -0.6493 -0.0336

5. Задать вектор-столбец свободных членов

>> b=[-0.800995;-5.7352459;-1.2411714]

b =

-0.8010

-5.7352

-1.2412

6. Вычислить значения коэффициентов a для каждого метрического пространства

>> alpha=Check(A)

alpha =

7. Найти решения системы линейных уравнений

>> LS_Iter(A,b,'Ro1',alpha(1),10^-6)

ans =

-4.8155

При решении системы линейных уравнений вычислительные формулы имеют вид:

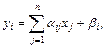(3.27)

где .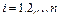

Из (3.27) видно, что в методе простой итерации для получения нового значения вектора решений на i +1-ом шаге используются значения переменных, полученные на предыдущем шаге.

Основная идея метода Зейделя состоит в том, что на каждом шаге итерационного процесса при вычислении значения переменной 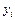учитываются уже найденные значения :

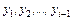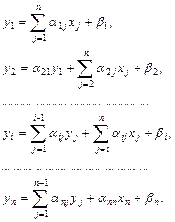(3.28)

Достаточные условия сходимости итерационного процесса (3.23)-(3.25) также являются достаточным условиями сходимости метода Зейделя.

Существует возможность автоматического преобразования исходной системы к виду, обеспечивающему сходимость итерационного процесса метода Зейделя. Для этого умножим левую и правую части системы (3.2) на транспонированную матрицу системы A^T, получим равносильную систему

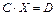, (3.29)

где , .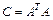

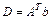Система (3.29) называется нормальной системой уравнений. Нормальные системы уравнений обладают рядом свойств, среди которых можно выделить следующие:

1) матрица C коэффициентов при неизвестных нормальной системы является симметрической (т.е. , );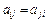

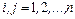2) все элементы, стоящие на главной диагонали матрицы C положительны (т.е. , ).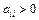

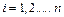Последнее свойство дает возможность «автоматически» приводить нормальную систему (3.29) к виду, пригодному для итерационного процесса Зейделя:

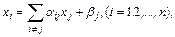(3.30)

где

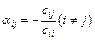, (3.31)

и

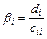. (3.32)

Целесообразность приведения системы к нормальному виду и использования метода Зейделя вытекает из следующей теоремы:

Теорема 3.2. Итерационный процесс метода Зейделя для приведенной системы (3.30), эквивалентной нормальной системе (3.29), всегда сходится к единственному решению этой системы при любом выборе начального приближения [2].

Таким образом решение произвольной системы линейных уравнений вида (3.1) методом Зейделя реализуется в соответствие со следующим алгоритмом:

1. Ввод матрицы А коэффициентов исходной системы и вектор-столбца свободных членов.

2. Приведение системы к нормальной умножением обеих частей системы на транспонированную матрицу А ^T.

3. Приведение нормальной системы к виду, пригодному для итерационного процесса Зейделя (3.30), (3.31).

4. Задание требуемой точности решения.

5. Циклическое выполнение итерационного процесса до достижения требуемой точности.

Для реализации метода Зейделя в пакете MATLAB необходимо:

1. Создать файл Zeidel.m, содержащий описание функции, выполняющей последовательно: а) приведение системы к нормальному виду; б) приведение нормальной системы к виду, пригодному для итерационного процесса Зейделя; в) реализацию итерационного процесса Зейделя.

% листинг файла Zeidel.m

function [z1,z2]=Zeidel(A,b,eps)

N=size(A,1);

% приведение системы к нормальному виду

C=A'*A;

D=A'*b;

% приведение системы к виду пригодному для итерационного процесса

% Зейделя

for i=1:N

D1(i)=D(i)/C(i,i);

end;

D1=D1'; % транспонирование матрицы

d1=D1;

for i=1:N

for j=1:N

if i==j

C1(i,j)=0;

Дата добавления: 2014-01-06