Hold on

plot(Y); % рис. 4.6

hold off;

plot(ff); % рис. 4.7

stairs(X,Y); % построение траектории итерационного процесса

% на плоскости XoY (рис. 4.8)

% построение траектории терационного процесса в трехмерном

% пространстве

plot3(X,Y,ff) % рис. 4.9

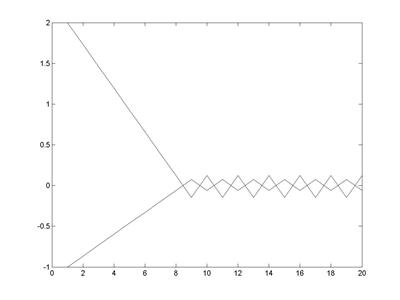
Рис. 4.6. Зависимость координат точки решения от номера итерации

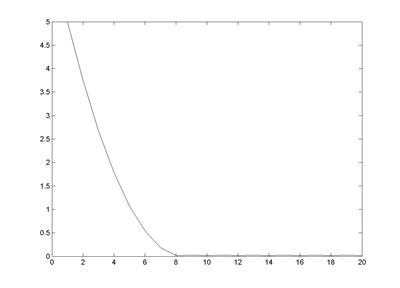
Рис. 4.7. Зависимость значения минимума функции от номера итерации

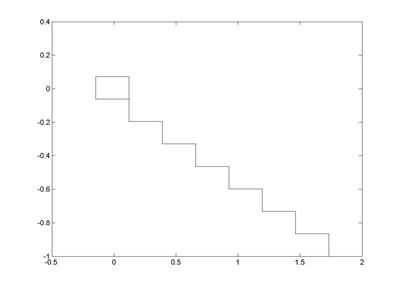
Рис. 4.8. Траектория итерационного процесса в плоскости XoY

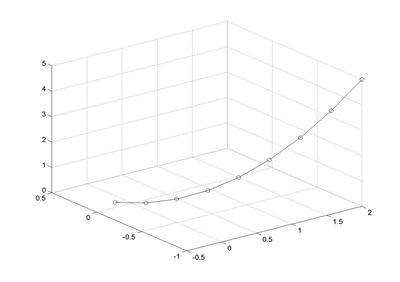
Рис. 4.9. Визуализация итерационного процесса в трехмерном пространстве

Пример 4.2. Алгоритм поиска экстремума с шагом, зависящим от свойств минимизируемой функции (использование производной по направлению).

Исследуем данный алгоритм применительно к минимизации функции двух переменных, заданной полиномом 4-го порядка:

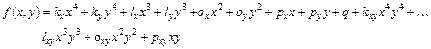
форма которой определяется коэффициентами kx, ky, lx, ly и т.д.

1. Создание файла F2_L4.m, содержащего описание функции, возвращающей значения функции f(x,y)

% листинг файла F2_L4.m

functionz=F2_L4(x,y,Lx,Ly,Ox,Px,Lxy,Oxy,Q,Kx,Ky,Oy,Py,Kxy,Pxy)

N=length(x);

z=zeros(N);

for i=1:N

for j=1:N

z(i,j)=Kx*x(i).^4+Ky*y(j).^4+Lx*x(i).^3+Ly*y(j).^3+Ox*x(i).^2+

Oy*y(j).^2 +Px*x(i)+Py*y(j)+Q+Kxy*x(i).^4*y(j).^4+

Lxy*x(i).^3*y(j).^3+Oxy*x(i).^2*y(j).^2+Pxy*x(i).*y(j);

end;

end;

2. Построение графика исследуемой функции при выбранных значения параметров

>> Lx=0.3;Ly=0.4;Ox=1;Px=1.2;Lxy=0.4;Oxy=0.3;Q=3;

>> Kx=0.5;Ky=1;Oy=2;Py=0.6;Kxy=0.2;Pxy=0.1;

>> Xmin=-1;Xmax=1;

>> Ymin=-1;Ymax=1;

>> N=23;

>> x(i)=Xmin+(Xmax-Xmin)/(N-1)*(i-1);

>> y(j)=Ymin+(Ymax-Ymin)/(N-1)*(j-1);

>> M=F2_L4(x,y,Lx,Ly,Ox,Px,Lxy,Oxy,Q,Kx,Ky,Oy,Py,Kxy,Pxy);

>> [X Y]=meshgrid(x,y);

>> surfc(X,Y,M)

Рис. 4.10

Анализ графика функции, представленной на рис. 4.10, показывает, график имеет «плато» - чрезвычайно пологое «дно». Понятно, что градиент в области «дна» будет иметь малую величину, поэтому можно ожидать, что алгоритмы с шагом, не зависящим от формы функции, будут иметь плохую сходимость.

3. Создание файлов g2_x.m, g2_y.m, содержащих описание функций, возвращающих значения частных производных

% листинг файла g2_x.m

function z=g2_x(x,y,Lx,Ly,Ox,Px,Lxy,Oxy,Q,Kx,Ky,Oy,Py,Kxy,Pxy)

N=length(x);

z=zeros(N);

for i=1:N

for j=1:N

z(i,j)=4*Kx*x(i).^3+3*Lx*x(i).^2+2*Ox*x(i)+Px... +4*Kxy*x(i).^3*y(j).^4+3*Lxy*x(i).^2*y(j).^3+2*Oxy*x(i).*y(j).^2+Pxy*y(j);

end;

end;

% листинг файла g2_y.m

function z=g2_y(x,y,Lx,Ly,Ox,Px,Lxy,Oxy,Q,Kx,Ky,Oy,Py,Kxy,Pxy)

N=length(x);

z=zeros(N);

for i=1:N

for j=1:N

z(i,j)=4*Ky*y(j).^3+3*Ly*y(j).^2+2*Oy*y(j)+...

Py+4*Kxy*x(i).^4*y(j).^3+3*Lxy*x(i).^3*y(j).^2+2*Oxy*x(i).^2*y(j)…

+Pxy*x(i);

end;

end;

4. Создание файла L2_Grad.m, содержащего описание скалярной функции, возвращающей, возвращающей значение длины градиента функции f (x, y)

% листинг функции L2_Grad.m

Дата добавления: 2014-01-06