Сплайн-интерполяция. Погрешность интерполяции

Погрешность интерполяции

Погрешность интерполяции полиномом Лагранжа оценивается по формуле:

, (5.22)

где

, (5.23)

. (5.24)

Погрешность интерполяции полиномом Ньютона оценивается по формулам:

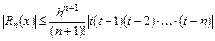, (5.25)

. (5.26)

При большом количестве узлов интерполяции приходится использовать интерполяционные полиномы высокой степени, что создает определенные неудобства при вычислениях. Можно избежать высокой степени интерполяционного многочлена, разбив отрезок интерполяции на несколько частей с построением на каждой части самостоятельного интерполяционного многочлена. Однако такое интерполирование обладает существенным недостатком: в точках сшивки разных интерполяционных полиномов будет разрывной их первая производная, поэтому для решения задачи кусочно-линейной интерполяции используют особый вид кусочно-полиномиальной интерполяции - сплайн-интерполяцию.

Сплайн - это функция, которая на каждом частичном отрезке интерполяции является алгебраическим многочленом, а на всем заданном отрезке непрерывна вместе с несколькими своими производными.

Пусть интерполируемая функция f (x) задана своими значениями в узлах , 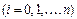. Обозначим длину частичного отрезка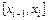 . Будем искать кубический сплайн на каждом из частичных отрезков 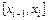в виде:

, (5.27)

где 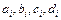- четверка неизвестных коэффициентов. Можно доказать, что задача нахождения кубического сплайна имеет единственное решение.

Потребуем совпадения значений в узлах с табличными значениями функции :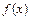

, (5.28)

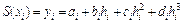. (5.29)

Число этих уравнений (2 n) в два раза меньше числа неизвестных коэффициентов. Для того чтобы получить дополнительные условия, потребуем также непрерывности первой и второй производных сплайна во всех точках, включая узлы. Для этого следует приравнять левые и правые производные 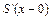, , , 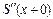во внутреннем узле .

Вычислив выражения для производных 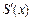, последовательным дифференцированием (5.27):

, (5.30)

, (5.31)

найдем правые и левые производные в узле:

,

,

где .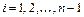

Аналогично поступаем для второй производной:

,

.

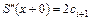Приравняв левые и правые производные, получаем:

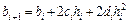, (5.32)

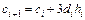, (5.33)

где .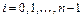

Уравнения (5.32), (5.33) дают еще 2(n -1) условий. Для получения недостающих уравнений накладывают требования к поведению сплайна на концах отрезка интерполяции. Если потребовать нулевой кривизны сплайна на концах отрезка интерполяции (т.е. равенство нулю второй производной), то получим:

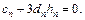, (5.34)

Исключив из уравнений (5.28)-(5.33) n неизвестных 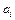, получаем систему уравнений:

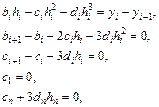(5.35)

где .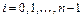

Система (5.35) состоит из 3 n уравнений. Решив систему (5.35), получаем значения неизвестных 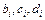, определяющих совокупность всех формул для искомого интерполяционного сплайна

(5.36)

где .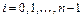

Программа, реализующая метод сплайн-интерполяции оказывается достаточно громоздкой, поэтому мы ограничимся обсуждением решения задачи об интерполяции синуса с помощью кубических сплайнов, используя функцию пакета MATLAB: spline ().

1. Задание табличных значений интерполируемой функции

>> N=8;

>> i=1:N;

>> x(i)=2*pi/(N-1)*(i-1);

>> y=sin(x);

2. Задание значения абсцисс точек, в которых вычисляется значение интерполяционного полинома

>> M=1000;

>> j=1:M;

>> X(j)=2*pi/(M-1)*(j-1);

>> Y=sin(X); % вычисление точных значений интерполируемой функции

4. Вычисление интерполируемых значений функции в узлах координатной сетки

>> yy=spline(x,y,X);

5. Визуализация результатов сплайн-интерполяции и разности между точными и интерполированными значениями (рис. 5.6, 5.7)

>> plot(x,y, 'o',X,yy);

>> plot(X,Y-yy);

6. Вычисление и визуализация значений первых производных сплайна (рис. 5.8)

>> m=1:M-1

>> yy1(m)=(yy(m+1)-yy(m))/(2*pi/(M-1));

>> plot(X(m),yy1(m))

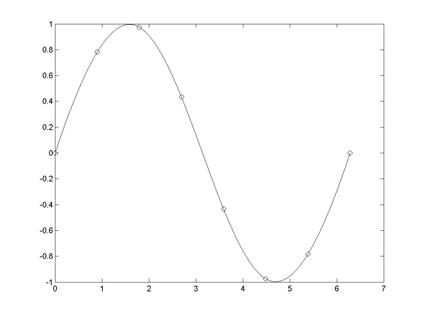
Рис. 5.6

Рис. 5.7

Рис. 5.8

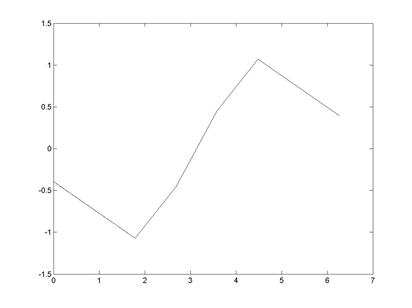
Рис. 5.9

7. Вычисление и визуализация значений вторых производных сплайна

>> m=1:M-2;

>> yy2(m)=(yy1(m+1)-yy1(m))/(2*pi/(M-1));

>> plot(X(m),yy2(m))

8. Вычисление значений и визуализация третьих производных сплайнов (рис. 5.10)

>> yy3(m)=(yy2(m+1)-yy2(m))/(2*pi/(M-1));

>> plot(X(m),yy3);

>> m=1:M-3;

Рис. 5.10

Как видно из рис. 5.7-5.10, первая и вторая производные сплайнов являются непрерывными функциями, третья и производные более высокого порядка - разрывными функциями.

Дата добавления: 2014-01-06