
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Аналитически
|
|
|
|
Численное дифференцирование функций, заданных
План
И ИНТЕГРИРОВАНИЕ
ЛЕКЦИЯ № 6. ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ
6.1. Численное дифференцирование функций, заданных аналитически
6.2. Особенности задачи численного дифференцирования функций, заданных таблично
6.3. Интегрирование функций, заданных аналитически (формула прямоугольников, формула трапеций, формула Симпсона)
6.4. Погрешность численного интегрирования
6.5. Вычисление интегралов методом Монте-Карло
По определению производная функции 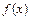
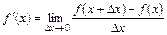 . (6.1)
. (6.1)
Переходя в (6.1) от бесконечно малых к конечным разностям, получаем приближенную формулу численного дифференцирования
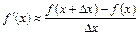 . (6.2)
. (6.2)
Формула (6.2) позволяет построить простой вычислительный алгоритм:
1) Задать значение точки, в которой вычисляется производная.
2) Задать значение приращение 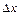 .
.
3) Вычислить производную в соответствие с формулой (6.2).
Замена бесконечно-малых приращений конечными является причиной возникновения ошибки. Для оценки ее величины разложим функцию 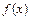 в точке
в точке 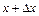 в ряд Тэйлора
в ряд Тэйлора
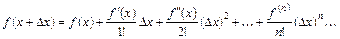 (6.3)
(6.3)
Подставив (6.3) в (6.4) и приведя подобные члены, получим
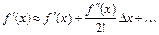 . (6.4)
. (6.4)
Из (6.4) видно, что все члены начиная с со второго, определяют отличие численного значения производной от ее точного значения. Основной член погрешности равен 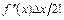 , т.к. данный член ~
, т.к. данный член ~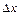 , говорят, что формула (6.2) имеет первый порядок точности по
, говорят, что формула (6.2) имеет первый порядок точности по 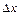 .
.
Можно вычислять производную, используя симметричную разностную схему:
 . (6.5)
. (6.5)
Для оценки точности данной формулы необходимо удержать в разложении в ряд Тэйлора первые четыре члена:
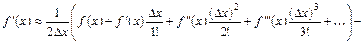
 . (6.6)
. (6.6)
Раскрыв в (6.6) скобки и приведя подобные, получаем:
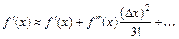 . (6.7)
. (6.7)
Из (6.7) видно, что основной член погрешности равен 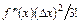 , т.к. данный член ~
, т.к. данный член ~  , говорят, что формула (6.5) имеет второй порядок точности по
, говорят, что формула (6.5) имеет второй порядок точности по 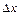 .
.
Пример 6.1. Численное дифференцирование функции 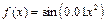 в пакете MATLAB:
в пакете MATLAB:
>> f=inline('sin(0.01*x.^2)'); % задание дифференцируемой
% функции
>> dx=0.01; % шаг изменения координатной сетки
>> x=0:dx:10*pi; % вычисление координат узлов
>> yf=feval(f,x); % вычисление значений функции в узлах
% выполнение процедуры численного дифференцирования
>> N=length(x);
>> m=1:N-1;
>> df(m)=yf(m+1)-yf(m)
>> plot(df) % визуализация производной функции (рис. 6.1)
>> f1=inline('0.02*x.*cos(0.01*x.^2)'); % задание функции,
% описывающей первую
% производную
>> ya=feval(f1,x); % вычисление значений первой производной по
% аналитической формуле
>> plot(x(m),abs(yf(m)-ya(m)); % визуализация разности между
% численными и аналитическими
% значениями производной (рис. 6.2)
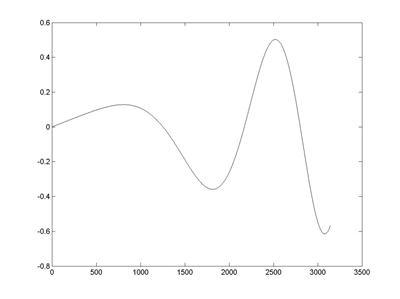
Рис. 6.1
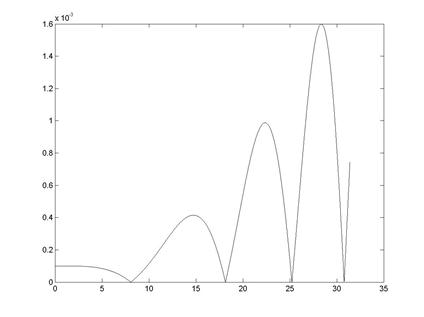
Рис. 6.2
Аналогичным образом поступают при вычислении производных высших порядков.
Отметим, что для аппроксимации производных конечными разностями в пакете MATLAB имеется функция diff().
Синтаксис функции:
>> diff(X) % возвращает конечные разности, вычисленные по
% смежным элементам вектора Х длина вектора,
% возвращаемого функцией diff(X) на единицу
% меньше длины вектора Х, если X - матрица
%, то возвращает матрицу, содержащую
% конечные разности, вычисленные по каждому столбцу
>> diff(X,n) % возвращает конечные разности n -го порядка
> > diff(X,n,dim) % возвращает конечные разности n -го порядка по
% столбцам (dim=1) или строкам матрицы
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 700; Нарушение авторских прав?; Мы поможем в написании вашей работы!