Вычисление интегралов методом Монте-Карло

Проиллюстрируем идеи метода Монте-Карло на примере вычисления определенного интеграла от функции, зависящей от одной переменной. Пусть нам необходимо вычислить интеграл (6.11) от некоторой заданной функции 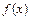на интервале 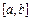. В предыдущем разделе мы рассмотрели несколько различных формул интегрирования, в которых использовались значения функции 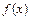, вычисляемые в равноотстоящих точках. Однако можно использовать и другой подход, суть которого легко понять из следующего примера.

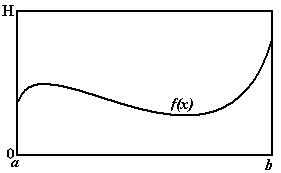
Рис. 6.6

Представим себе прямоугольник высотой H и длиной b - a такой, что функция 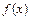целиком лежит внутри данного прямоугольника (рис. 6.6). Сгенерируем N пар случайных чисел, равномерно распределенных в данном прямоугольнике:

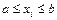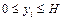,. (6.29)

Тогда доля точек , удовлетворяющих условию 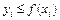, является оценкой отношения интеграла от функции 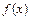к площади рассматриваемого прямоугольника. Следовательно, оценка интеграла в данном методе может быть получена по формуле

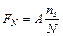, (6.30)

где - число точек, удовлетворяющих условию 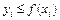, N - полное количество точек, A - площадь прямоугольника.

Можно предложить и другой путь вычисления определенного интеграла, рассматривая его как среднее значение функции 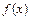на отрезке :

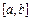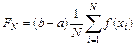, (6.31)

где - последовательность случайных чисел с равномерным законом распределения на отрезке .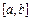

Отметим, что в отличие от данных методов погрешность метода Монте-Карло не зависит от размерности и меняется как 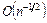. Следовательно, для достаточно больших d интегрирование по методу Монте-Карло будет приводить к меньшим погрешностям при тех же значениях N.

Пример 6.6. Вычисление интеграла 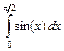методом Монте-Карло в пакете MATLAB:

% задание координат вершит прямоугольника

>> Xmin=0;

>> Xmax=pi/2;

>> Ymin=0;

>> Ymax=1.5;

% генерация случайных координат

>> N=2000;

>> x=Xmin+(Xmax-Xmin)*rand(N,1);

>> y=Ymin+(Ymax-Ymin)*rand(N,1);

% подсчет числа точек, попавших под график функции

>> s=0;

>> for i=1:N

if y(i)<=feval(f,x(i))

s=s+1;

end;

end;

>> s*(Xmax-Xmin)*(Ymax-Ymin)/N % вычисление значения

% интеграла

ans =

Дата добавления: 2014-01-06