Одномерная оптимизация

Все пошаговые методы оптимизации состоят из двух важнейших частей:

- выбора направления,

- выбора шага в данном направлении (подбор коэффициента обучения).

Методы одномерной оптимизации дают эффективный способ для выбора шага.

В простейшем случае коэффициент обучения фиксируется на весь период оптимизации. Этот способ практически используется только совместно с методом наискорейшего спуска. Величина подбирается раздельно для каждого слоя сети по формуле

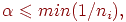
где 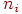обозначает количество входов -го нейрона в слое.

Более эффективный метод основан на адаптивном подборе коэффициента 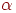с учетом фактической динамики величины целевой функции. Стратегия изменения значения 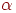определяется путем сравнения суммарной погрешности 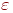на 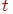-й итерации с ее предыдущим значением, причем рассчитывается по формуле

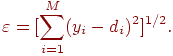
Для ускорения процесса обучения следует стремиться к непрерывному увеличению 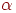при одновременном контроле прироста погрешности 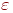по сравнению с ее значением на предыдущем шаге. Незначительный рост погрешности считается допустимым.

Если погрешности на 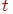-1-й и 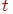-й итерациях обозначить соответственно 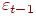и 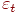, а коэффициенты обучения на этих же итерациях — 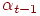и 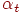, то значение 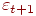следует рассчитывать по формуле

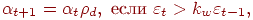
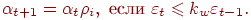
где 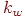- коэффициент допустимого прироста погрешности, 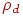- коэффициент уменьшения 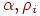- коэффициент увеличения .

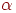Наиболее эффективный, хотя и наиболее сложный, метод подбора коэффициентов обучения связан с направленной минимизацией целевой функции в выбранном направлении 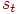. Необходимо так подобрать значение 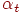, чтобы новое решение 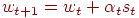соответствовало минимуму целевой функции в данном направлении .

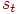Поиск минимума основан на полиномиальной аппроксимации целевой функции. Выберем для аппроксимации многочлен второго порядка

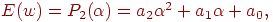
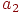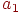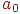где , и — коэффициенты, определяемые в цикле оптимизации. Для расчета этих коэффициентов используем три произвольные точки 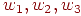, лежащие в направлении 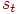, т.е.

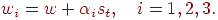
Соответствующие этим точкам значения целевой функции 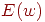обозначим как

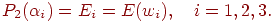(5)

Коэффициенты 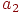, 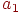и 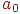рассчитываются в соответствии с решением системы уравнений (5). Для определения минимума многочлена 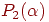его производная 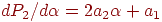приравнивается к нулю, что позволяет получить 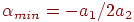. После подстановки выражений для 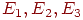в формулу для получаем

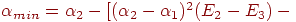
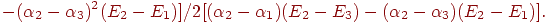
Дата добавления: 2014-01-06