Радиальная нейронная сеть

Использование в разложении 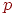базисных функций, где 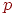- это количество обучающих выборок, недопустимо также и с практической точки зрения, поскольку обычно количество этих выборок очень велико, и в результате вычислительная сложность обучающего алгоритма становится чрезмерной. Решение системы уравнений (1) размерностью 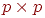при больших значениях 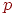становится затруднительным. Так же, как и для многослойных сетей, необходимо редуцировать количество весов, что в этом случае сводится к уменьшению количества базисных функций. Поэтому отыскивается субоптимальное решение в пространстве меньшей размерности, которое с достаточной точностью аппроксимирует точное решение. Если ограничиться базисными функциями, то аппроксимирующее решение можно представить в виде

(3)

где 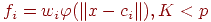, а - множество центров, которые необходимо определить. В особом случае, если принять , можно получить точное решение .

Чаще всего в качестве радиальной функции применяется функция Гаусса. При размещении ее центра в точке она может быть определена в сокращенной форме как

(4)

В этом выражении - параметр, от значения которого зависит ширина функции.

Полученное решение, представляющее аппроксимирующую функцию в многомерном пространстве в виде взвешенной суммы локальных базисных радиальных функций (выражение (3)), может быть интерпретировано радиальной нейронной сетью, представленной на рис. 2 (для упрощения эта сеть имеет только один выход), в которой определяется зависимостью (4). Это сеть с двухслойной структурой, в которой только скрытый слой выполняет нелинейное отображение, реализуемое нейронами с базисными радиальными функциями. Выходной нейрон, как правило, линеен, а его роль сводится к взвешенному суммированию сигналов, поступающих от нейронов скрытого слоя. Вес 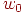, как и при использовании сигмоидальных функций, представляет поляризацию (порог), вводящую показатель постоянного смещения функции.

Рис. 2. Обобщенная структура радиальной сети

Полученная архитектура радиальных сетей имеет структуру, аналогичную многослойной структуре сигмоидальных сетей с одним скрытым слоем. Роль скрытых нейронов в ней играют базисные радиальные функции, отличающиеся своей формой от сигмоидальных функций. Несмотря на отмеченное сходство, сети этих типов принципиально отличаются друг от друга. Радиальная сеть имеет фиксированную структуру с одним скрытым слоем и линейными выходными нейронами, тогда как сигмоидальная сеть может содержать различное количество слоев, а выходные нейроны бывают как линейными, так и нелинейными. У используемых радиальных функций может быть весьма разнообразная структура. Нелинейная радиальная функция каждого скрытого нейрона имеет свои значения параметров и , тогда как в сигмоидальной сети применяются, как правило, стандартные функции активации с одним и тем же для всех нейронов параметром 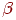. Аргументом радиальной функции является эвклидово расстояние образца от центра , а в сигмоидальной сети - это скалярное произведение векторов .

Дата добавления: 2014-01-06