Алгоритмы уточнения корня

1. Алгоритм уточнения корня методом половинного деления

Сущность метода. Пусть каким-либо методом найден отрезок изоляции корня [а; b] уравнения F(х) = 0, где F(х) - непрерывна на участке [a; b], (а)*F(b) < 0. В дальнейшем требуется сузить этот отрезок так, чтобы его длина стала не больше заранее заданной точности вычисления корня e, то есть чтобы |b - a| £ e.

Этот процесс сужения интервала, содержащего изолированный корень уравнения F(х) = 0, называется уточнением корня.

В этом алгоритме отрезок изоляции корня [а; b] точкой с = 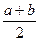делят пополам и вычисляют значение F(c). Если F(c) = 0, то с - значение искомого корня уравнения, и задача решена. Если F(c) ¹ 0, то искомый корень уравнения содержится в одном из двух отрезков [a; c] или [c; b], на концах которого функция F принимает значения разных знаков. Обозначим этот отрезок через [a₁, b₁], его длина b₁-a₁ = 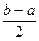. С отрезком [a₁, b₁] поступают точно так, как и с отрезком [a, b]. Этот процесс последовательного деления отрезка пополам продолжают до тех пор, пока не произойдет одно из двух:

§ либо найдется такая точка c_n = 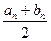, в которой F(c_n) = 0 (что маловероятно!), и задача решена;

§ либо такой точки не найдется, но при некотором n придем к отрезку [a_n, b_n] длины b_n - a_n = 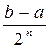£ e, содержащему в себе искомый корень.

Тогда числа a_n и b_n являются приближенными значениями искомого корня с требуемой точностью e соответственно с недостатком и с избытком. Однако лучше за приближенное значение искомого корня взять число с_n = 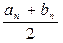, погрешность которого не превышает .

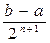2. Алгоритм уточнения корня методом хорд

Сущность метода. Пусть отрезок изоляции [a; b] корня х уравнения F(х) = 0 найден, причем для определенности пусть F(a) < 0, F(b) > 0 и F'(х) > 0. График функции y = F(х) проходит через точки A(a; F(a)) и B(b; F(b)) (рис. 1). Составим уравнение хорды АВ как прямой, проходящей через точки А и В:

y = kx + l;

F(a) = ka + l;

F(b) = kb + l;

k = 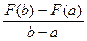; l = F(a) - a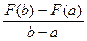

y=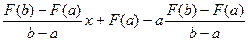

y - F(a) = 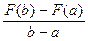(x - a).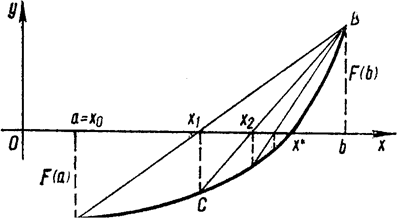

Рисунок 1 – Графическое представление метода хорд

далее находим абсциссу x₁ точки пересечения хорды АВ с осью Ох, уравнение которой y = 0: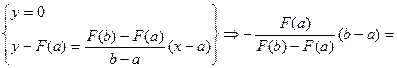

= x₁ - a Þ x₁ = a - .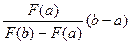

Число x₁ примем за первое приближение корня х*. Далее, применяя этот же прием к отрезку изоляции [x₁; b], на концах которого функция F(x) принимает противоположные знаки, получим второе приближение корня x₂:

x₂ = x₁ -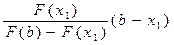

Этот процесс можно продолжать неограниченно. Описанный процесс называется методом хорд. В результате получим последовательность вложенных отрезков[a; b] É [x₁; b] É [x₂; b] É... É [x_n; b] É ... с неподвижным концом b. Последовательные приближения x_n (n = 1, 2,...) к точному значению корня х* вычисляются по формуле

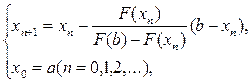(3)

называемой формулой метода хорд, и образуют монотонно возрастающую последовательность a = x₀ < x₁ < x₂ <... < x_n < x_n+1 <... < b, ограниченную сверху числом b. По теореме Вейерштрасса эта последовательность имеет предел

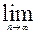x_n = *.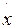

Поскольку F(х) непрерывна на [а; b], то 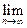F(x_n) = F(^*).

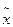Переходя теперь к пределу в равенстве (3), получаем

^* = ^* -

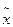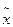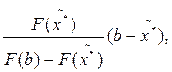
откуда, так как b - 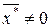, следует, что F(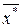) = 0. Но в связи с тем, что уравнение F(x) = 0 на отрезке [а; b] имеет единственный корень х *, то х * = х *.

Поскольку полученная последовательность (х„) сходится к корню уравнения х *, то любой ее член можно рассматривать в качестве приближенного значения корня. Практически последовательные приближения вычисляют до тех пор, пока не получат приближенное значение корня с требуемой точностью.

3. Алгоритм уточнения корня методом касательных

Сущность метода. Пусть [а; b] — отрезок изоляции корня х * уравнения F(х) = 0. И пусть для определенности F(a)<0, F(b)>0, F‘(x) > 0 и F ” (x) > 0, xÎ[а; b], то есть производные сохраняют постоянный знак (рис.2). Идея метода касательных, предложенного Ньютоном, сводится к замене небольшой дуги

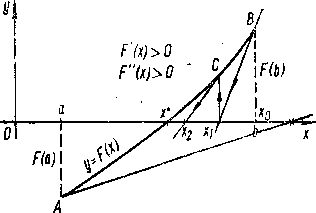
Рисунок 2 – Графическое представление метода касательных

кривой у = F(х) касательной к кривой, проведенной в некоторой точке интервала [а; b]. Выберем, например, x₀ = b, так как F(x₀) ´ F¢¢(x₀)>0, и в точке В(x₀, F(х₀)) проведем касательную к кривой у = F(х). Ее уравнение:

y - F(x₀) = F¢(x₀)(x - x₀). '

Найдем теперь точку пересечения x₁ касательной с осью Ох (у = 0):

0 - F(x₀) = F¢(x₀)(x₁ - x₀) Þ x₁ = x₀ -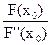

Эту точку x₁ принимаем за первое приближение искомого корня х *. Через точку С(x₁; F(x₁)) снова проведем касательную y - F(x₁) = F‘(x₁)(x - x₁), абсциссу точки пересечения которой с осью Ох примем за второе приближение х₂ корня х *. Имеем:

0 - F(x₁) = F‘(x₁)(x₂ - x₁) Þ x₂ = x₁ -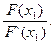

Продолжая этот процесс далее, получим рекуррентную формулу,

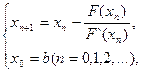(8)

называемую формулой метода касательных.

Заметим, что если в рассматриваемом случае (F’(x) > О, F”(x) > О, F(b) > 0, F(а) < 0) касательную провести в точке А, то есть положить x₀ = а, то точка пересечения ее с осью абсцисс может оказаться вне отрезка изоляции корня [a; b]. Это значит, что метод касательных неприменим, если в качестве начальной точки x₀ выбрать такую, в которой F(x₀) ´ F”(x₀) < 0.

Как и в методе хорд, можно доказать (предлагаем читателю сделать это самостоятельно), что полученная числовая последовательность

x₀>x₁>x₂>...>x_n>x_n+1>...>a

сходится к корню уравнения х *.

Для оценки погрешности приближения x_n можно воспользоваться, как и в методе хорд, формулой

½x* - x_n½ £ ½x_n - x_n-1½ £ e.

Анализируя возможные расположения кривой у = F(х) на отрезке изоляции, где последовательные приближения по методу касательных обозначены (i = 0,1,2...), получаем правило для использования метода касательных: в качестве начального приближения x₀ выбирается тот конец отрезка изоляции (x₀ = а или x₀ = b), в котором выполняется условие

F(x₀) F¢¢(x₀) > 0 (9)

Пример 9. Методом касательных найти корень уравнения

F(x) =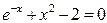

на отрезке [1; 2] с точностью до e = 10^-5.

Находим: F‘(x) = -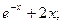F¢¢(x) = .

Применив формулу (8), имеем:

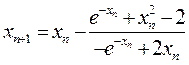(n = 0, 1, 2,...).

Выберем начальное приближение x₀, используя условие (9). Имеем:

F(1) = 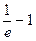< 0;

F(2) = > 0;

F¢¢(1) = > 0;

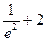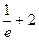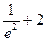F¢(2) = >0.

Поскольку F(2)´F”(2) > 0, то касательную следует проводить в правом конце отрезка, то есть x₀ = b = 2.

Последовательные приближения вычисляем на ЭВМ, заполняя табл. 7.

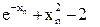
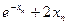
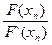
	Xn	F(xn)=	F‘(xn)=		½ xn – xn-1 ½
	(2) - (5)		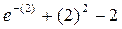e^-(2)+2×(2)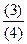
	2,0	2,135335	3,864665	0,552528
	1,5	0,473130	2,776870	0,170382	0,5
	1.38	0,033377	2,395523	0,013933	0,17
	1,316	0,000062	2,363794	0,000026	0,014
	1,8159738	0.0000005	2,3637346	0,0000002	0,0000262
	1,3159736	- 0,0000005	2,3637342	-0,0000002	0,0000002

Если в качестве приближенного значения корня взять число 1,3159736, то невязка F(1,3159737) = - 0,0000003.

4. Комбинированный метод хорд и касательных

Сущность метода. Рассмотренные выше метод хорд и метод касательных (каждый в отдельности) позволяют приблизиться к корню уравнения лишь с одной стороны: либо слева (приближение с недостатком), либо справа (приближение с избытком), причем всегда, если формула хорд дает приближение корня с недостатком, то формула касательных — с избытком, и наоборот. Одновременное применение этих двух методов на каждом шаге дает возможность искомый корень уравнения взять в вилку и не выпускать его из нее до достижения заданной точности.

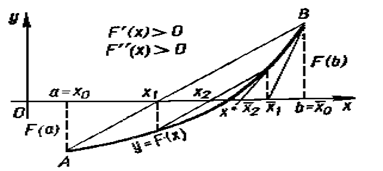
Рисунок 3 – Иллюстрация метода хорд и касательных

Пусть (рис.3) условие F()×F«() > 0 выполняется в правом конце отрезка изоляции корня (= b). Тогда последовательные значения с недостатком х₀ = а, x₁, x₂,..., x_n, x_n+1,... вычисляют методом хорд:

x_n+1 = x_n - 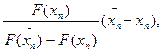x₀ = a(n = 0, 1, 2,...), (10)

а последовательные значения корня с избытком

= b,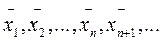

вычисляют методом касательных (8):

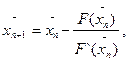
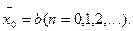(11)

По формулам (10) и (11) вычисляют приближенные значения корня соответственно с недостатком и с избытком, причем для всех n x_n < х* < х_n.

Если при некотором n выполняется неравенство 0 < ½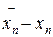½ £ e то в качестве приближенного значения искомого корня с точностью e принимают среднее арифметическое значение полученных двусторонних приближений, то есть x =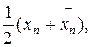так как тогда½x - x^*½ < ½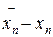½ £ e.

Если условие 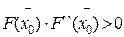выполняется в левом конце отрезка изоляции корня, тогда

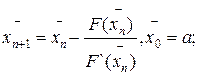(12)

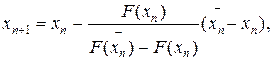x₀ = b (n = 0,1,2,...), (13)

то есть формула касательных дает приближение корня с недостатком, а формула хорд—с избытком.

Обращаем внимание читателя на следующее обстоятельство. Если в формулах (3) и (7) метода хорд (его иногда называют стационарным методом хорд) один конец отрезка изоляции корня в процессе вычислений все время оставался неподвижным, то в формулах (10) и (13) комбинированного метода хорд и касательных оба конца отрезка изоляции корня являются подвижными. На каждом шаге вычислений в качестве неподвижного конца формулы метода хорд используется приближенное значение искомого корня, вычисленное по формуле метода касательных (рис. 22).

Дата добавления: 2014-01-06