Постановка задачи. Понятие об электронной подписи

ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ

Понятие об электронной подписи

Мы рассмотрели, как клиент может переслать организации свои конфиденциаль­ные данные (например, номер электронного счета). Точно так же он может общаться и с банком, отдавая ему распоряжения о перечислении своих средств на счета других лиц и организаций. Ему не надо ездить в банк и стоять в очереди — все можно сделать, не отходя от компьютера. Однако здесь возникает проблема: как банк узнает, что распоряжение поступило именно от данного лица, а не от злоумышленника, выдающего себя за него? Эта проблема решается с помощью так называемой элек­тронной подписи.

Принцип ее создания тот же, что и рассмотренный выше. Если нам надо создать себе электронную подпись, следует с помощью специальной программы (получен­ной от банка) создать те же два ключа: закрытый и публичный. Публичный ключ передается банку. Если теперь надо отправить поручение банку на операцию с рас­четным счетом, оно кодируется публичным ключом банка, а своя подпись под ним кодируется собственным закрытым ключом. Банк поступает наоборот. Он читает поручение с помощью своего закрытого ключа, а подпись — с помощью публичного ключа поручителя. Если подпись читаема, банк может быть уверен, что поручение ему отправили именно мы, и никто другой.

Вопросы для самоконтроля

1. Какие угрозы безопасности информации вы знаете?

2. Какие типы вирусов вы знаете, и какую угрозу они несут?

3. Какие меры следует предпринять для обеспечения безопасности информации?

4. Какие антивирусные программы вы знаете?

5. В чем заключаются особенности обработки конфиденциальной информации, с т.з. обеспечения ее безопасности?

6. Что такое электронная подпись?

Задача численного интегрирования функции заключается в вычислении определенного интеграла на основании ряда значений подынтегральной функции. Численное вычисление однократного интеграла называется механической квадратурой.

Мы будем рассматривать способы приближенного вычисления определенных интегралов

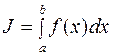, (10.1)

основанные на замене интеграла конечной суммой:

, (10.2)

где С_k - числовые коэффициенты, а x_k Î [ a, b ], k = 0, 1, …, n.

Приближенное равенство

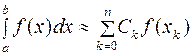(2.3)

называется квадратурной формулой, а x _k – узлами квадратурной формулы. Погрешность квадратурной формулы определяется соотношением

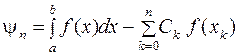. (10.4)

В общем случае погрешность квадратурной формулы (2.4) зависит как от выбора коэффициентов С_к , так и от расположения узлов х_к. Введем на отрезке [ a, b ] равномерную сетку с шагом h, тогда x_i = a + ih, где (i = 0, 1,..., n;
h·n = b-a). Теперь выражение (2.1) можно представить в виде суммы интегралов по частичным отрезкам:

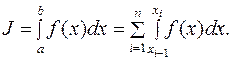(10.5)

Таким образом, для построения формулы численного интегрирования на отрезке [ a, b ] достаточно построить квадратурную формулу на частичном отрезке [ x_i-1, x_i ] и воспользоваться формулой (2.5).

Дата добавления: 2014-01-06