Формула Симпсона

В этом методе предлагается подынтегральную функцию на частичном отрезке аппроксимировать параболой, проходящей через точки
(x_j, f (x_j)), где j = i -1; i -0.5; i, то есть подынтегральную функцию аппроксимируем интерполяционным многочленом Лагранжа второй степени:

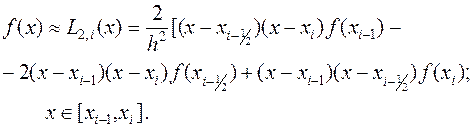(10.14)

Проведя интегрирование, получим:

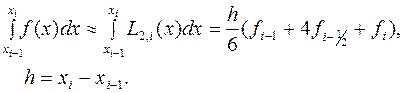
(10.15)

Это и есть формула Симпсона или формула парабол. На отрезке
[ a, b ] формула Симпсона примет вид

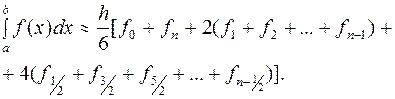(10.16)

Графическое представление метода Симпсона показано на рис. 2.4.

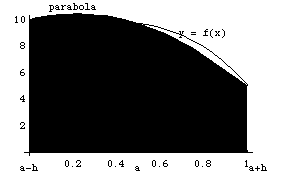
Рис. 10.4. Метод Симпсона

Избавимся в выражении (2.16) от дробных индексов, переобозначив переменные:

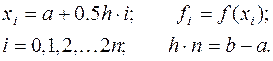(10.17)

Тогда формула Симпсона примет вид

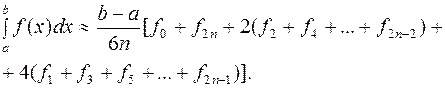(10.18)

Погрешность формулы (2.18) оценивается следующим выражением:

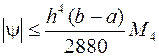, (10.19)

где h·n = b - a, 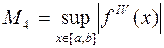. Таким образом, погрешность формулы Симпсона пропорциональна O (h⁴).

Замечание. Следует отметить, что в формуле Симпсона отрезок интегрирования обязательно разбивается на четное число интервалов.

10.5. Вычисление определенных интегралов методами
Монте–Карло

Рассматриваемые ранее методы называются детерминированными, то есть лишенными элемента случайности.

Методы Монте–Карло (ММК) – это численные методы решения математических задач с помощью моделирования случайных величин. ММК позволяют успешно решать математические задачи, обусловленные вероятностными процессами. Более того, при решении задач, не связанных с какими-либо вероятностями, можно искусственно придумать вероятностную модель (и даже не одну), позволяющую решать эти задачи. Рассмотрим вычисление определенного интеграла

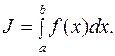(10.20)

При вычислении этого интеграла по формуле прямоугольников интервал [ a, b ] разбиваем на N одинаковых интервалов, в серединах которых вычислялись значения подынтегральной функции. Вычисляя значения функции в случайных узлах, можно получить более точный результат:

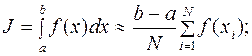(10.21)

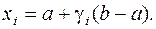(10.22)

Здесь γ_i - случайное число, равномерно распределенное на интервале
[0, 1]. Погрешность вычисления интеграла ММК ~ 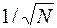, что значительно больше, чем у ранее изученных детерминированных методов.

На рис. 2.5 представлена графическая реализация метода Монте-Карло вычисления однократного интеграла со случайными узлами (2.21) и (2.22).

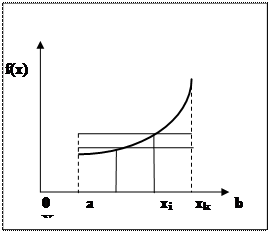Рис. 10.5. Интегрирование методом Монте-Карло (1-й случай)

Однако при вычислении кратных интегралов детерминированными методами оценка погрешности перерастает в задачу порой более сложную, чем вычисление интеграла. В то же время погрешность вычисления кратных интегралов ММК слабо зависит от кратности и легко вычисляется в каждом конкретном случае практически без дополнительных затрат.

Рассмотрим еще один метод Монте-Карло на примере вычисления однократного интеграла:

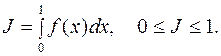(2.23)

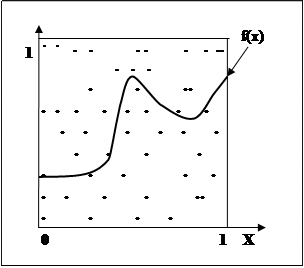
Рис. 10.6. Интегрирование методом Монте-Карло (2-й случай)

Как видно на рис. 2.6, интегральная кривая лежит в единичном квадрате, и если мы сумеем получать пары случайных чисел, равномерно распределенных на интервале [0, 1], то полученные значения (γ_1, γ₂) можно интерпретировать как координаты точки в единичном квадрате. Тогда, если этих пар чисел получено достаточно много, можно приблизительно считать, что
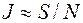. Здесь S – число пар точек, попавших под кривую, а N – общее число пар чисел.

Пример 2.1. Вычислить следующий интеграл:

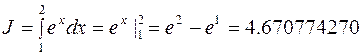
Поставленная задача была решена различными методами. Полученные результаты сведены в табл. 2.1.

Таблица 2.1

Число интервалов (точек)	Метод левых прямоугольников	Метод средних прямоугольников	Метод правых прямоугольников	Метод трапеций	Метод Симпсона	Метод Монте-Карло
	4.44112722	4.66882868	4.90820465	4.25683746	4.67077443	4.62289422
	4.64745932	4.67075481	4.69416706	4.62903035	4.67077427	4.69812790

Замечание. Выбор табличного интеграла позволил нам сравнить погрешность каждого метода и выяснить влияние числа разбиений на точность вычислений.

11 ПРИБЛИЖЕННОЕ РЕШЕНИЕ НЕЛИНЕЙНЫХ
И ТРАНСЦЕНДЕНТНЫХ УРАВНЕНИЙ

Дата добавления: 2014-01-06