Комбинированный метод

Пусть f (a) ·f (b) < 0, а f¢(x) и f¢¢ (x) сохраняют постоянные знаки на отрезке [ a¸ b ]. Соединяя метод хорд и метод касательных, получаем метод, на каждом шаге которого находим значения по недостатку и значения по избытку точного корня ξуравнения f (x) = 0. Теоретически здесь возможны четыре случая:

· f¢(x) > 0; f¢¢ (x) > 0;

· f¢(x) > 0; f¢¢ (x) < 0;

· f¢(x) < 0; f¢¢ (x) > 0;

· f¢(x) < 0; f¢¢ (x) < 0.

Рассмотрим только первый случай, так как остальные три ведут себя аналогично и могут быть сведены к первому.

Итак, пусть f¢ (x) > 0 и f¢¢ (x) > 0при 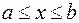. Полагаем, что 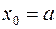(для метода хорд), 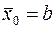(для метода касательных). Тогда новые значения корня вычисляем по формулам

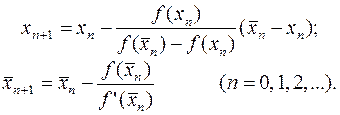(11.18)

Рис. 11.4 наглядно иллюстрирует суть комбинированного метода.

Рис. 11.4. Уточнение корня комбинированным методом

Доказано, что 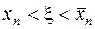. Следует обратить внимание на то, что на каждом шаге метод хорд применяется к новому отрезку . Если задать максимальное значение погрешности ε > 0, процесс уточнения значения корня продолжаем до тех пор, пока не выполнится условие

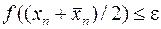. (11.19)

Пример 11.1. Вычислить с точностью до 0.0005 положительный корень уравнения

f(x) = x⁵ – x – 0.2 = 0.

На первом этапе отделения корней выбрали интервал [1.0, 1.1], на концах которого функция имеет противоположные знаки. Действительно,
f (1) = – 0.2 < 0, f (1.1) = 0.31051 > 0. В выбранном нами интервале f¢¢ (x) > 0, f¢¢ (x) > 0, то есть знаки производных сохраняются.

Применим комбинированный метод, приняв . По формулам (4.18) вычислим

.

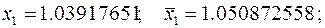
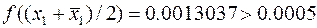Так как точность недостаточная (погрешность велика), вычислим следующие значения:

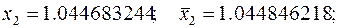
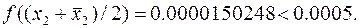
Таким образом, за два шага мы обеспечили требуемую точность.

Дата добавления: 2014-01-06