Объявления и определения (расширенное рассмотрение)

Понятие о варианте и инварианте цикла

При разработке циклов в последнее время все чаще используются понятия варианта и инварианта цикла. Основным из этих двух понятий является понятие инварианта цикла. Понятие варианта цикла используется реже: его применяют совместно с инвариантом цикла.

Вариант цикла — неотрицательное выражение, результат вычисления которого уменьшается на каждом шаге цикла.

Инвариант цикла — это логическое высказывание (утверждение), истинность которого должна быть обеспечена в следующих точках цикла:

· вначале работы цикла (после выполнения его инициализации),

· в конце каждого шага (перед очередным тестированием условия, проверяемого в цикле).

Выполнение этих двух условий должно гарантировать выполнение инварианта после окончания работы цикла.

Вариант и инвариант цикла принято оформлять в виде комментариев в тексте программы, предшествующем циклу.

Назначение рассматриваемых понятий является:

· Помочь программисту организовать цикл.

· Повысить читабельность программного кода.

· Помочь программисту убедиться в правильности работы цикла.

Пример 1. Вычисление суммы квадратов натуральных чисел.

Постановка задачи. Вычислить сумму квадратов первых n напуральных чисел.

Алгоритм решения этой задачи приведен в п. 1. 26 первой части пособия. Напишем вариант и инвариант цикла для программы, выполняющей необходимые вычисления.

Вариантом цикла в рассматриваемом примере может служить выражение n – i + 1, а инвариантом цикла — утверждение: просуммированы квадраты всех натуральных чисел из диапазона [1, i - 1]. На каждом шаге цикла его вариант цикла численно равен количеству чисел, квадраты которых следует суммировать, а инвариант содержит оценку диапазона чисел, для которых такое суммирование уже выполнено.

Напишем программу, снабдив ее комментариями, содержащими вариант и инвариант цикла. Кроме того, в программе помощью комментариев будут отмечены точки, в которых должна иметь место истинность инварианта цикла. При использовании для организации цикла инструкции for такие точки должны находиться внутри заголовка цикла. Первая из точек должна находиться после выражения инициализации, а вторая после выражения, определяющего продвижение цикла.

#include<stdio.h>
int main(void)
{
int i, n, s;
printf(“n=”);
scanf(“%d”, &n);

/* Вариант: n – i + 1 */
/*
Инвариант цикла: Просуммированы все числа из диапазона
[1, i - 1]
*/

s = 0;
for (i = 1 /* Инвариант истинен */; i <= n;
i++ /* Инвариант истинен */

)

s += i * i; /* Инвариант ложен */

/* Можно сделать вывод, что инвариант здесь истинен */
printf(“Сумма квадратов =%d”, s);
getch();

return 0;
}

Проанализируем работу цикла, воспользовавшись понятиями варианта и инварианта. Для определенности будем полагать, что переменная “n” после выполнения операции ввода имеет значение, равное 3.

После инициализации цикла искомая сумма, представленная переменной s, обнуляется, а счетчик цикла (переменная i) оказывается равным 1. Выбранные инициализирующие значения переменных i и s обеспечивают истинность инварианта после выполнения выражения инициализации (i = 1) инструкции for. Действительно, для i == 1 диапазон чисел ([1, i - 1]), квадраты которых просуммированы, оказывается пустым. То положение, что сумма s пустого диапазона равна нулю, обеспечивает истинность инварианта цикла в рассматриваемой точке цикла. Вариант цикла (n – i + 1) в этой точке оказывается равным 3.

На каждом шаге цикла его вариант уменьшается на 1 и на 1 увеличивается диапазон просуммированных квадратов чисел. После окончания работы цикла параметр цикла i == n + 1. С учетом этого вариант цикла в этой точке будет равен нулю, истинность инварианта цикла будет свидетельствовать о том, что все квадраты чисел из заданного по условию задачи диапазона [1, 3] просуммированы.

Предположим теперь, что при программировании цикла была допущена ошибка, состоящая в том, что в заголовке цикла (инструкции for) в качестве логического выражения вместо правильного отношения i <= n было написано i < n. В этом случае после окончания работы цикла параметр цикла окажется равным n. С учетом этого вариант цикла в этой точке будет равен единице, истинность инварианта цикла будет свидетельствовать о том, что просуммированы квадраты чисел только из диапазона [1, 2]. Это позволяет сделать вывод о том, что квадрат одного числа остался не учтенным. Это позволит устранить допущенную ошибку в организации цикла.

Пример 2. Возведение в целочисленную степень.

Постановка задачи. Пусть требуется вычислить значение выражения 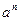, не прибегая к использованию стандартной функции pow(). Будем считать основание степени a вещественным, а показатель n – неотрицательным целым числом.

Рассмотрим три различных варианта рещения рассматриваемой задачи. Каждый из вариантов решения будет иметь свой инвариант цикла. Дадим вначале общую характеристику предлагаемых решений.

В двух первых способах решение строится с использованием арифметического цикла, а в третьем способе для этих целей используется итерационный цикл.

Первый вариант решения. Наиболее очевидное решение может быть получено с учетом следующего соотношения

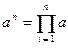
В этом случае возведение в степень может быть заменено многократным умножением на основание степени. С этой целью введем переменную p, с помощью которой будем накапливать произведение. Ниже приводится фрагмент программы, выполняющей необходимые вычисления. После завершения цикла переменная p должна содержать искомый результат вычислений.

// Инвариант p ==

p = 1.0;
for(int i = 0 /* Инв */; i!= n; i++ /* Инв */)

p *= a;

Второй вариант решения. Для нахождения искомого результата воспользуемся следующей идеей. Заменим вычисление исходного выражения 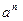многократным (циклическим) вычислением выражения p * . В цикле необходимо уменьшать значение показателя k на 1 и увеличивать значение множителя p. Для обеспечения корректности такой замены достаточно при организации цикла потребовать выполнения следующего инварианта цикла: p * == 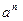. Цикл должен закончить свою работу в момент, когда переменная k станет равной нулю. Тогда переменная p будет содержать искомый результат вычислений. Ниже приводится фрагмент программы, реализующий вычисление

// Инвариант p * == 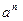, p – вычисленная часть степени
p = 1.0;
int k = n;
// Инв.
while(k!= 0)
{

p *= a;
k--;
// Инв.
}

Третий вариант решения.

// Инвариант p * b ==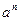
p = 1.0;
int k = n;
double b = a;
while(k!= 0)
{
if(k % 2 == 1)
{

p *= b;
k--;
}else
{
b *= b;
k /= 2;
}
}

Объявления и определения уже обсуждались в первой части настоящего пособия в пункте 1.12. Рассмотрение этого вопроса ограничивалось наиболее простыми вариантами их применений, в которых объявлялись простые переменные встроенных типов. Во второй части пособия должны изучаться более сложные программные элементы (функции, указатели, массивы). В связи с этим представляется целесообразным вновь вернуться к рассмотрению этого вопроса.

В общем случае объявление программного элемента состоит из двух структурных частей:

· последовательности спецификаторов.

· списка описателей; элементы списка отделяются запятыми

Вначале объявления должна записываться последовательность спецификаторов, а затем список объявителей. Число объявителей в списке определяется числом, объявляемых имен. Объявляемое имя в качестве необязательного компонента может иметь список инициализаторов.

Дата добавления: 2014-01-06