
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Совершенная дизъюнктивная нормальная форма (СДНФ) и совершенная конъюнктивная нормальная форма (СКНФ)
|
|
|
|
Если логическая функция представлена дизъюнкцией, конъюнкцией и инверсией, то такая форма представления называется нормальной.
Элементарная конъюнкция — конъюнкция конечного множества логических переменных и их инверсий.
Элементарная дизъюнкция — дизъюнкция конечного множества логических переменных и их инверсий.
Число аргументов, образующих элементарную дизъюнкцию или конъюнкцию, называется ее рангом.
Пример 1. Х & Y & Z, Х &. Y & Z — элементарные конъюнкции третьего ранга. Х v Y, Х v Y — элементарные дизъюнкции второго ранга.
Дизъюнктивная нормальная форма (ДНФ) содержит элементарные конъюнкции, связанные между собой операцией дизъюнкции.
Конъюнктивная нормальная форма (КНФ) содержит элементарные дизъюнкции, связанные между собой операцией конъюнкции.
Одну и ту же логическую функцию можно представить разными ДНФ и КНФ.
Пример 2. Нетрудно убедиться (построив таблицы истинности для каждой из логических формул или проведя преобразования на основании логических законов), что приведенные ниже формулы определяют одну и ту же логическую функцию F(X, Y, Z):
1) 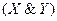 Ú
Ú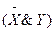 Ú
Ú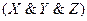 ;
;
2) 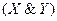 Ú
Ú
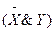 Ú
Ú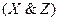 .
.
Для исключения неоднозначности записи логические функции могут быть представлены в совершенных дизъюнктивной и конъюнктивной нормальных формах.
Совершенная дизъюнктивная нормальная форма (СДНФ) отвечает следующим требованиям:
1) в ней нет двух одинаковых элементарных конъюнкций;
2) ни одна элементарная конъюнкция не содержит двух одинаковых переменных;
3) ни одна элементарная конъюнкция не содержит переменную вместе с ее инверсией;
4) все конъюнкции имеют один и тот же ранг.
Аналогичным требованиям подчиняется и совершенная конъюнктивная нормальная форма (СКНФ).
Пример 3. Если логическая функция содержит конъюнкции разных рангов, то для получения СДНФ следует повысить ранг младших конъюнкций, используя закон исключения третьего.
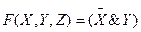 Ú
Ú Ú
Ú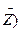 Ú
Ú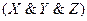
 Ú
Ú Ú
Ú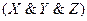 .
.
СДНФ и СКНФ можно получить по табличному представлению логической функции.
5.5.1. Алгоритм образования СДНФ по таблице истинности
1. Выделить в таблице истинности все наборы переменных, на которых функция принимает единичные значения.
2. Для каждого выбранного набора записать элементарные конъюнкции, содержащие без инверсии переменные, принимающие в соответствующем наборе значение 1 и с инверсией —
переменные, принимающие значение 0.
3. Соединить элементарные конъюнкции знаком дизъюнкции.
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 1671; Нарушение авторских прав?; Мы поможем в написании вашей работы!