
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 10. Прикладная психолингвистика
|
|
|
|
Тема 7
Дефибриллятор.
Цикл реанимации – это комплекс последовательных реанимационных мероприятий продолжительностью 4-5 мин, который включает в себя приемы СЛР, медикаментозной и электроимпульсной реанимации. Если было проведено последовательно 2-5 циклов реанимации без положительного ответа, то реанимационное пособие можно прекращать.
Плоские волны в однородной изотропной среде
Поляризация волн
Ориентация векторов 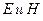 относительно осей
относительно осей 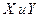 в плоской волне, в момент
в плоской волне, в момент 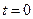 распространяющейся вдоль оси
распространяющейся вдоль оси 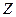 , зависит от источника, создающего волну. Пусть, например, волна создается элементарным электрическим вибратором, расположенным на оси
, зависит от источника, создающего волну. Пусть, например, волна создается элементарным электрическим вибратором, расположенным на оси 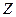 параллельно оси X в среде без потерь. Тогда в области, примыкающей к оси Z и удовлетворяющей условиям, при которых сферическую волну можно приближенно считать плоской, вектор
параллельно оси X в среде без потерь. Тогда в области, примыкающей к оси Z и удовлетворяющей условиям, при которых сферическую волну можно приближенно считать плоской, вектор  будет иметь одну составляющую
будет иметь одну составляющую 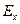 , а вектор
, а вектор 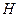 -только составляющую
-только составляющую 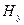 .
.
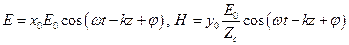 , где
, где 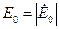 (1)
(1)
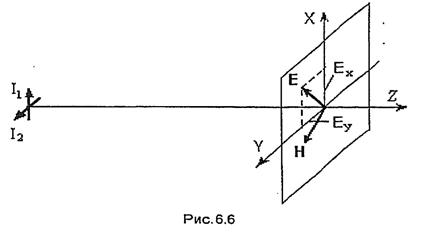
|
Так как векторы 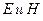 взаимосвязаны (
взаимосвязаны (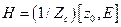 ), ограничимся рассмотрением одного вектора
), ограничимся рассмотрением одного вектора  . Из формулы (1) следует, что половину периода направление вектора
. Из формулы (1) следует, что половину периода направление вектора  совпадает с направлением оси
совпадает с направлением оси 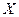 , а другую половину периода – противоположно. Таким образом, в фиксированной точке пространства (
, а другую половину периода – противоположно. Таким образом, в фиксированной точке пространства (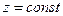 ) конец вектора
) конец вектора  с течением времени перемещается вдоль отрезка прямой линии, а величина вектора изменяется в интервале
с течением времени перемещается вдоль отрезка прямой линии, а величина вектора изменяется в интервале 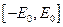 . Волны, обладающие таким свойством, принято называть линейно поляризованными. Плоскость, проходящую через ось
. Волны, обладающие таким свойством, принято называть линейно поляризованными. Плоскость, проходящую через ось 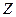 и вектор
и вектор  , называют плоскостью поляризации. В рассматриваемом примере плоскостью поляризации является плоскость
, называют плоскостью поляризации. В рассматриваемом примере плоскостью поляризации является плоскость 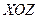 .
.
Если источником волны является элементарный магнитный вибратор, параллельный оси 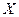 , или элементарный электрический вибратор, параллельный оси
, или элементарный электрический вибратор, параллельный оси 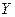 , то вектор
, то вектор  имеет только составляющую
имеет только составляющую 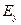 , а вектор
, а вектор 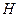 - только составляющую
- только составляющую 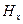 . Волна в этом случае также будет линейно поляризованной.
. Волна в этом случае также будет линейно поляризованной.
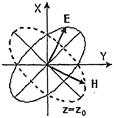
Предположим теперь, что волна создается двумя вибраторами, например взаимно перпендикулярными элементарными электрическими вибраторами, расположенными на оси 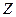 , как показано на рис.18. В этом случае вектор
, как показано на рис.18. В этом случае вектор  имеет две составляющие
имеет две составляющие 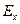 и
и 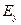 , которые изменяются либо синфазно, либо с некоторым фазовым сдвигом в зависимости от соотношения между фазами токов вибраторов. Вектор
, которые изменяются либо синфазно, либо с некоторым фазовым сдвигом в зависимости от соотношения между фазами токов вибраторов. Вектор 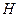 при этом имеет также две составляющие
при этом имеет также две составляющие 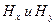 . Таким образом, в общем случае выражение для вектора
. Таким образом, в общем случае выражение для вектора  плоской волны в среде без потерь записывается в виде
плоской волны в среде без потерь записывается в виде
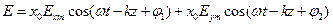 (2)
(2)
|
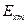 и
и 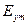 - амплитуды составляющих
- амплитуды составляющих 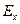 и
и 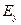 соответственно, a
соответственно, a 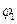 и
и 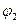 -фазы этих составляющих в точке z = 0 при t = 0. Для перехода к случаю среды с отличной от нуля проводимостью нужно в (2) заменить
-фазы этих составляющих в точке z = 0 при t = 0. Для перехода к случаю среды с отличной от нуля проводимостью нужно в (2) заменить 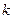 на
на 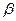 и положить
и положить 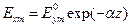 и
и 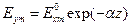 , где
, где 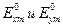 - значения амплитуд составляющих
- значения амплитуд составляющих 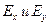 соответственно в плоскости
соответственно в плоскости  . При этом получим
. При этом получим
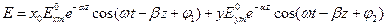 (3)
(3)
Формулы (2) и (3) однотипны, и для дальнейшего достаточно исследовать любую из них, например (3). Волну (3) можно рассматривать как суперпозицию двух плоских линейно поляризованных волн с взаимно перпендикулярной ориентацией векторов  , распространяющихся в одном направлении (вдоль оси
, распространяющихся в одном направлении (вдоль оси 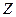 ). Характер изменения вектора
). Характер изменения вектора  волны (3) с течением времени в фиксированной точке пространства зависит от соотношения между начальными фазами
волны (3) с течением времени в фиксированной точке пространства зависит от соотношения между начальными фазами 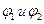 и от амплитуд
и от амплитуд 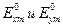 .
.
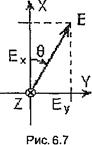
Угол 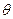 (19) между осью X и вектором
(19) между осью X и вектором  в фиксированной точке пространства (
в фиксированной точке пространства (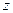 ) определяется соотношением
) определяется соотношением
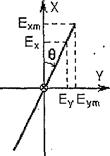
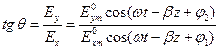 (4)
(4)
Как следует из формулы (4), угол 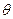 зависит от соотношения между
зависит от соотношения между 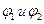 , а также от отношения
, а также от отношения 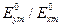 . В общем случае угол
. В общем случае угол 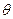 может изменяться со временем. Предположим, что начальные фазы
может изменяться со временем. Предположим, что начальные фазы 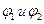 совпадают. Полагая в формуле (4)
совпадают. Полагая в формуле (4) 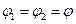 , получаем
, получаем
|
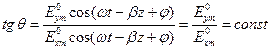 (5)
(5)
Следовательно, вектор Е, определяемый равенством (3) в любой момент времени, лежит в плоскости, проходящей через ось Z и составляющей угол 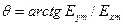 с плоскостью
с плоскостью 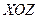 (рис. 20).
(рис. 20).
Аналогичное явление имеет место также в том случае, когда разность между 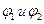 равна целому числу
равна целому числу 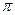 :
:
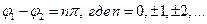 (6)
(6)
В фиксированной точке пространства конец вектора  с течением времени перемещается вдоль отрезка прямой линии, составляющей с осью
с течением времени перемещается вдоль отрезка прямой линии, составляющей с осью 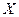 угол
угол 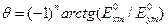 . Таким образом, волна (3) при выполнении условия (6) является линейно поляризованной. Очевидно, что поворотом осей координат
. Таким образом, волна (3) при выполнении условия (6) является линейно поляризованной. Очевидно, что поворотом осей координат 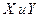 относительно оси
относительно оси 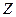 в этом случае можно добиться того, чтобы вектор
в этом случае можно добиться того, чтобы вектор  в новой системе координат имел только одну составляющую
в новой системе координат имел только одну составляющую 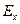 или
или 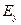 .
.
Рассмотрим второй частный случай. Пусть амплитуды составляющих 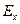 и
и 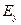 равны, а начальные фазы отличаются на
равны, а начальные фазы отличаются на 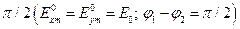 . Тогда
. Тогда 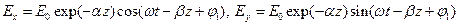 . Подставляя эти выражения в (4), получаем равенство
. Подставляя эти выражения в (4), получаем равенство
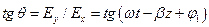 , откуда следует, что
, откуда следует, что
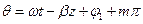 где
где 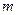 - целое число. (7)
- целое число. (7)
Равенство (7) означает, что угол 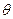 в фиксированной точке пространства (z) увеличивается пропорционально f. Величина вектора Е при этом остается неизменной: |Е| =Е0.
в фиксированной точке пространства (z) увеличивается пропорционально f. Величина вектора Е при этом остается неизменной: |Е| =Е0.
Таким образом, в фиксированной точке пространства вектор  , оставаясь неизменным по величине, вращается с угловой частотой
, оставаясь неизменным по величине, вращается с угловой частотой 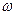 вокруг направления
вокруг направления 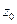 . Конец вектора
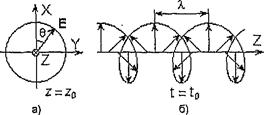
. Конец вектора  при этом описывает окружность (рис. 21, а). Волны такого типа называют волнами с круговой поляризацией.
при этом описывает окружность (рис. 21, а). Волны такого типа называют волнами с круговой поляризацией.
Нетрудно убедиться в том, что при 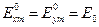 волна будет иметь круговую поляризацию, если
волна будет иметь круговую поляризацию, если
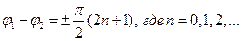 (8)
(8)
|
В зависимости от направления вращения вектора  различают волны с правой и левой круговой поляризацией. В случае правой круговой поляризации вектор
различают волны с правой и левой круговой поляризацией. В случае правой круговой поляризации вектор  вращается по часовой стрелке (если смотреть вдоль направления распространения волны), а в случае левой круговой поляризации - против часовой стрелки.
вращается по часовой стрелке (если смотреть вдоль направления распространения волны), а в случае левой круговой поляризации - против часовой стрелки.
В рассмотренном примере (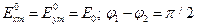 ) волна имеет правую круговую поляризацию. Очевидно, что такая же поляризация будет и в том случае, если
) волна имеет правую круговую поляризацию. Очевидно, что такая же поляризация будет и в том случае, если
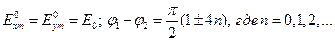 (9)
(9)
При выполнении условий
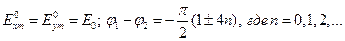 (10)
(10)
волна имеет левую круговую поляризацию.
Таким образом, вектор  вращается в направлении от опережающей по фазе составляющей вектора
вращается в направлении от опережающей по фазе составляющей вектора  к отстающей. На рис.21,б показана ориентация вектора
к отстающей. На рис.21,б показана ориентация вектора  , соответствующего различным значениям координаты
, соответствующего различным значениям координаты 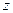 в фиксированный момент времени, для случая плоской волны с круговой поляризацией, распространяющейся в среде без потерь. Линия, соединяющая концы векторов, является винтовой линией с шагом, равным длине волны. Ее проекция на плоскость
в фиксированный момент времени, для случая плоской волны с круговой поляризацией, распространяющейся в среде без потерь. Линия, соединяющая концы векторов, является винтовой линией с шагом, равным длине волны. Ее проекция на плоскость 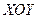 образует окружность (рис.21, а). С течением времени изображенная на рис.21,6 винтовая линия, определяющая ориентацию вектора Е в зависимости от координаты
образует окружность (рис.21, а). С течением времени изображенная на рис.21,6 винтовая линия, определяющая ориентацию вектора Е в зависимости от координаты 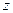 , вращается вокруг оси
, вращается вокруг оси 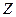 с угловой частотой
с угловой частотой 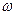 . В случае среды без потерь этот процесс можно трактовать и как перемещение винтовой линии вдоль оси
. В случае среды без потерь этот процесс можно трактовать и как перемещение винтовой линии вдоль оси 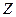 со скоростью
со скоростью 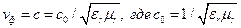 - скорость света в вакууме.
- скорость света в вакууме.
В случае среды с потерями линия, соединяющая концы векторов  , вычисленных в один и тот же момент времени в разных точках оси
, вычисленных в один и тот же момент времени в разных точках оси 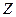 , представляет собой спираль, радиус которой (расстояние от оси
, представляет собой спираль, радиус которой (расстояние от оси 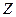 до спирали) изменяется вдоль
до спирали) изменяется вдоль 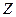 по закону
по закону 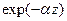 .
.
Отметим, что винтовая линия, соответствующая волне с правой круговой поляризацией, имеет левую намотку, и, наоборот, в случае волны с левой круговой поляризацией винтовая линия имеет правую намотку.
Из проведенного анализа следует, что любая волна круговой поляризации является суперпозицией двух линейно поляризованных волн. Покажем, что всякую линейно поляризованную волну можно представить в виде суммы двух волн с круговой поляризацией. Пусть вектор  линейно поляризованной волны колеблется в плоскости
линейно поляризованной волны колеблется в плоскости 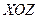 .
.
Комплексная амплитуда вектора  в этом случае имеет вид
в этом случае имеет вид
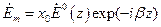 (11)
(11)
где 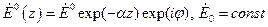 . В результате получим
. В результате получим
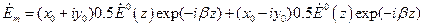 (12)
(12)
Первое слагаемое в правой части равенства (12) описывает волну с левой круговой поляризацией, а второе - волну с правой круговой поляризацией.
В общем случае вектор  определяется формулой (3). В фиксированной точке пространства он изменяется и по величине, и по направлению. Найдем форму линии, описываемой при этом концом вектора
определяется формулой (3). В фиксированной точке пространства он изменяется и по величине, и по направлению. Найдем форму линии, описываемой при этом концом вектора  . Введя обозначение
. Введя обозначение 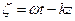 , получим из (3) следующие соотношения:
, получим из (3) следующие соотношения:
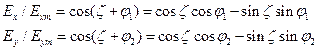 (13)
(13)
где 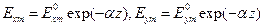 . Решая систему уравнений (13), имеем
. Решая систему уравнений (13), имеем
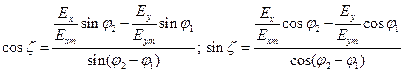
Возводя обе части этих уравнений в квадрат и почленно складывая получающиеся выражения, прихожим к уравнению
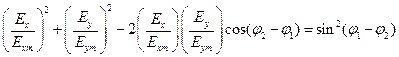
описывающему эллипс, большая ось которого повернута относительно оси  на угол
на угол  (рис.6.10), определяемый соотношением
(рис.6.10), определяемый соотношением
|
 (14)
(14)
В случае среды с потерями получается аналогичный результат. Отличие состоит лишь в том, что величины полуосей эллипса зависят от координаты  (уменьшаются с увеличением
(уменьшаются с увеличением  ).
).
Таким образом, в общем случае, т.е. при произвольных 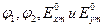 в фиксированной точке пространства (z) конец вектора Е описывает эллипс. Волны такого типа принято называть эллиптически поляризованными. Ориентация векторов
в фиксированной точке пространства (z) конец вектора Е описывает эллипс. Волны такого типа принято называть эллиптически поляризованными. Ориентация векторов  , соответствующих различным значениям координаты
, соответствующих различным значениям координаты 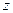 в фиксированный момент времени в среде без потерь, аналогична изображенной на рис.21,б. Отличие состоит в том, что в данном случае проекция винтовой линии, соединяющей концы векторов
в фиксированный момент времени в среде без потерь, аналогична изображенной на рис.21,б. Отличие состоит в том, что в данном случае проекция винтовой линии, соединяющей концы векторов  , на плоскость
, на плоскость 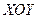 образует эллипс (рис. 22).
образует эллипс (рис. 22).
Очевидно, что линейно поляризованная волна и волна с круговой поляризацией являются частными случаями эллиптически поляризованной волны. Отметим, что понятие линейной, круговой и эллиптической поляризации применимо не только для плоских, но и для других типов волн. Например, сферические волны, создаваемые в дальней зоне элементарным электрическим вибратором или элементарным магнитным вибратором, являются линейно поляризованными. Действительно, в случае ЭЭВ вектор  колеблется в меридианальной плоскости, и в любой фиксированной точке пространства, принадлежащей дальней зоне, его направление либо совпадает с направлением вектора
колеблется в меридианальной плоскости, и в любой фиксированной точке пространства, принадлежащей дальней зоне, его направление либо совпадает с направлением вектора 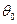 , либо противоположно ему. Аналогично в случае элементарного магнитного вибратора вектор
, либо противоположно ему. Аналогично в случае элементарного магнитного вибратора вектор  лежит в азимутальной плоскости, и в любой фиксированной точке направлен либо так же, как вектор
лежит в азимутальной плоскости, и в любой фиксированной точке направлен либо так же, как вектор 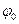 , либо противоположно ему.
, либо противоположно ему.
Волны, созданные более сложными излучателями, могут иметь и круговую, и эллиптическую поляризацию. Например, сферическая волна, создаваемая в дальней зоне двумя взаимно перпендикулярными элементарными электрическими вибраторами, токи которых равны по величине и сдвинуты по фазе на 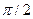 , в направлении, перпендикулярном обоим вибраторам, будет иметь круговую поляризацию.
, в направлении, перпендикулярном обоим вибраторам, будет иметь круговую поляризацию.
При определении поляризации волны до сих пор рассматривался только вектор  . Очевидно, такой же анализ для вектора Р привел бы к аналогичным результатам. В общем случае (при прозвольных начальных фазах и амплитудах) конец вектора
. Очевидно, такой же анализ для вектора Р привел бы к аналогичным результатам. В общем случае (при прозвольных начальных фазах и амплитудах) конец вектора 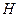 в фиксированной точке пространства с течением времени также описывает эллипс, подобный эллипсу вектора
в фиксированной точке пространства с течением времени также описывает эллипс, подобный эллипсу вектора  и повернутый относительно него на угол
и повернутый относительно него на угол 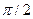 (рис.22). В рассмотренных выше частных случаях линейной и круговой поляризацией этот эллипс вырождается соответственно в отрезок прямо линии и окружность.
(рис.22). В рассмотренных выше частных случаях линейной и круговой поляризацией этот эллипс вырождается соответственно в отрезок прямо линии и окружность.
Отметим, что в тех случаях, когда анализируемая плоская волна является неоднородной (т.е. когда поверхности равных амплитуд не совпадают с поверхностями равных фаз), поляризация волны может быть различной в разных точках плоскости, перпендикулярной направлению распространения волны (оси 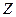 ). Это объясняется тем, что амплитуда неоднородной плоской волны зависит от координат
). Это объясняется тем, что амплитуда неоднородной плоской волны зависит от координат 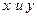 и при изменении последних может изменяться соотношение между составляющими
и при изменении последних может изменяться соотношение между составляющими 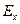 и
и 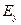 . Кроме того, поляризация неоднородной волны, определенная по вектору
. Кроме того, поляризация неоднородной волны, определенная по вектору  , может не совпадать с поляризацией волны по вектору
, может не совпадать с поляризацией волны по вектору 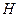 .
.
Выясним условие взаимной перпендикулярности векторов  и
и 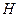 плоской волны. В общем случае имеют место соотношения
плоской волны. В общем случае имеют место соотношения
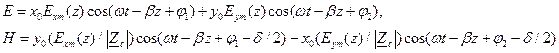 (15)
(15)
Перемножая скалярно выписанные выражения для векторов Е и Н, после несложных преобразований получаем
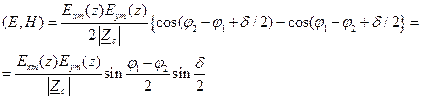 (16)
(16)
Для ортогональности векторов необходимо, чтобы их скалярное произведение было равно нулю. Правая часть равенства (16) обращается в нуль только в следующих частных случаях: при 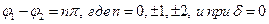
Первый случай соответствует линейно поляризованной волне, а второй - среде без потерь.
Таким образом, в общем случае векторы 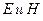 в среде с потерями не перпендикулярны друг другу. Это вызвано тем, что в среде с потерями векторы
в среде с потерями не перпендикулярны друг другу. Это вызвано тем, что в среде с потерями векторы 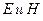 изменяются несинфазно.
изменяются несинфазно.
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 405; Нарушение авторских прав?; Мы поможем в написании вашей работы!