Проведение опыта. Рассмотрим объект – игральную кость из 6 граней (цифры от 1 до 6)

Рассмотрим объект – игральную кость из 6 граней (цифры от 1 до 6). Её бросают. Кость может перейти в одно из состояний с соответствующим числом на верхней грани – всего их будет 6. Причём вероятность выпадения любой грани одинакова и равна в данном случае 1/6.

До бросания объект может находиться в неопределённом состоянии – одном из 6 возможных.

Обозначим эту неопределённость через H. Ясно, что чем больше возможных состояний N, тем больше величина H, но конкретный вид этой функции предстоит определить:

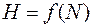, (1)

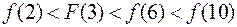(2)

Во время опыта субъект получает количество информации I. Эта информация снимает неопределённость знания об объекте у наблюдателя. Очевидно, количество информации равно разности неопределённостей знания до и после опыта:

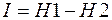
Но, внимание! После опыта наблюдатель знает об объекте всё – то есть H₂ =0! Значит, информация, полученная через опыт (или, как говорят, заключённая в опыте) равна исходной неопределённости.

Теперь назовём исходную неопределённость информационной энтропией и получим классическую формулировку:

«Количество полученной информации об объекте совпадает с первоначальной (доопытной) энтропии объекта»

Осталось определить вид функции f в формуле (1). Чтобы сделать это, надо определить её свойства для усложненных объектов. Один из таких – рассмотреть объект из нескольких одинаковых игральных костей.

При этом опыт заключается в последовательном подбрасывании каждой кости. Теперь нельзя сказать, что число возможных состояний равно 6 для нашей шестигранной кости. Обозначим число возможных состояний сложного объекта из M костей через X. Простыми рассуждениями легко определить возможное число состояний для объектов из разного числа костей M:

M	X-число состояний
…	…
M	6^M

Снова вернёмся к вопросу определения вида функции f для расчёта количества энтропии. Поскольку все кости (отдельные части сложного объекта) независимы, то самым естественным условием для функции является условие аддитивности, а именно – энтропия сложного объекта равна сумме энтропий каждого из них. Для случая игральной кости:

H_M =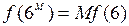=6 H₁ (3)

Аналогичную формулу можно написать для сложной системы, состоящей из объектов с числом равновероятных состояний N. Данное свойство называется свойством аддитивности.

Функцией, удовлетворяющей данному свойству, будет функция, равная логарифму от X.

f = k * log_осн (X) (4)

Эту формулу можно упростить. За единицу энтропии естественно ту, которая имеет минимальную значению. Такая энтропия (минимальная неопределённость) будет у объекта, который имеет всего два состояния в условиях опыта описанного выше для игральной кости. Если бы у объекта было бы только одно состояния, то не было бы никакой определённости и H =0.

Поэтому для основания 2 и значении k =1, получаем формулу Хартли:

H = log₂ (X) (5)

Итак, подведём итог.

В качестве единицы информации принимается, связанное с проведением опыта, состоящего в получении одного из двух равновероятных исходов (примером такого опыта является бросание монеты, при которым возможны два равновероятных исхода: «орёл» или «решка»).

Такая единица количества информации называется «бит».

Дата добавления: 2014-01-06