Оно вновь не оптимально

Элементы разрешающей строки делим на разрешающий элемент и все элементы разрешающего столбца (кроме разрешающего элемента) обнуляем. Результаты записываем в новую симплекс- таблицу.

В последней, оценочной строке, указаны коэффициенты целевой функции с противоположными знаками.

Менеджеру фирмы требуется составить оптимальный план выпуска изделий из условия максимальной прибыли.

Построение математической модели:

х₁, х₂, х₃ – количество изделий каждого вида.

6х₁ + 5х₂ + 4х₃ ≤ 120

3х₁ + 2х₂ + 4х₃ ≤ 96

5х₁ + 3х₂ + 3х₃ ≤ 180

х₁, х₂, х₃ ≥ 0

F= 9х₁ + 10х₂ + 16х₃ → max

1. Приводим задачу к каноническому виду:

6х₁ + 5х₂ + 4х₃ + х₄ = 120

3х₁ + 2х₂ + 4х₃ + х₅ = 96

5х₁ + 3х₂ + 3х₃ + х₆ = 180

х₁,.. х₆ ≥ 0

F= 9х₁ + 10х₂ + 16х₃ → max

2. Составляем исходную симплекс-таблицу (заметим, что в разных учебных пособиях форма симплекс- таблицы различна!):

Базисн. перем.	х1	х2	х3	х4	х5	х6	вi	Оцен. отн.
х4
х5
х6
Оцен. строка	-9	-10	-16

В первом столбце указаны базисные переменные. Напомним, что им в матрице системы соответствует определитель не равный нулю (набор единичных столбцов в таблице). В столбце в_i указаны правые части уравнений, а в последнем столбце – оценочное отношение (смысл поясним позже).

По составленной таблице прочитаем исходное опорное решение (исходную угловую точку):

х₁ = (0,0,0,120,96,180).

Понятно, что в самой таблице указана матрица системы ограничений.

3. Проверяем опорное решение на оптимальность: если все элементы оценочной строки неотрицательны, то опорное решение оптимально. В нашем случае это не так.

4. В оценочной строке находим наименьший отрицательный элемент. Соответствующий столбец назовем разрешающим.

5. Заполняем оценочное отношение, деля элементы столбца в_i на элементы разрешающего столбца (учитываются только положительные элементы, в противном случае, ставится прочерк).

6. Находим минимальное оценочное отношение. Соответствующий элемент разрешающего столбца выделяем и называем разрешающим. (строку, в которой находится разрешающий элемент называем разрешающей).

Остальные элементы таблицы пересчитываем по правилу прямоугольника и также записываем в новую таблицу.

Правило прямоугольника поясним схемой: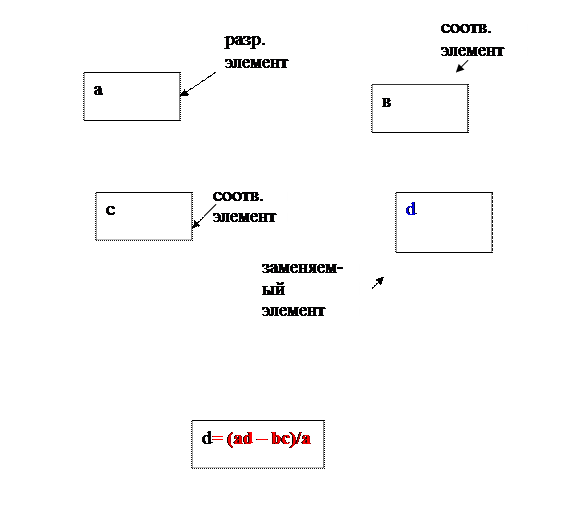

Базисн. перем.	х1	х2	х3	х4	х5	х6	вi	Оцен. отн.
х4					-1
х3	3/4	1/2			1/4
х6	11/4	3/2			-3/4
Оцен. строка		-2

8) Новое опорное решение х₂ = (0, 0, 24, 24, 0, 108).

Перейдя к п.4) получим уже последнюю таблицу:

Базисн. перем.	х1	х2	х3	х4	х5	х6	вi	Оцен. отн.
х2				1/3	-1/3
х3	1/4			-1/6	5/12
х6	5/4			-1/2	-1/4
Оцен. строка				2/3	10/3

Новое опорное решение х₃ = (0, 8, 20, 0, 0, 96). F_max = 400

Итак, х₃ оптимальное решение. Следуя ему, нужно выпускать 8 единиц 2-го изделия и 20- третьего. Выпуск 1-го изделия экономически не выгоден. Ожидаемая максимальная прибыль 400 у.е.

Заметим, также, что т.к. х₄ = х₅ = 0, а х₆ = 96, то следуя оптимальному решению первый и второй ресурсы будут израсходованы полностью (т.е. они дефицитны), а третий ресурс будет не доиспользован в количестве 96. (не дефицитен).

Отметим также, что в оценочной строке последней таблицы

х₁ = 5. Экономический смысл: если, все - таки, включить в оптимальный план первое изделие, то прибыль уменьшится на 5 у.е.

Замечания

Дата добавления: 2014-01-06