Римская система записи

Непозиционные системы счисления

Непозиционные - алфавит которых содержит неограниченное количество символов, причем количественный эквивалент любой цифры постоянен, и зависит только от ее начертания. Позиция цифр в числе значения не имеет.

Непозиционные системы строятся по принципу аддитивности (англ. Add - сумма) - количественный эквивалент числа определяется как сумма цифр.

Алфавитная система записи чисел

В Малой Азии, где были древнегреческие колонии, которые вели оживленную торговлю, в середине V в. до н. э. появилась система счисления нового типа - так называемая алфавитная нумерация. Ее обычно называют ионийской. В этой системе числа обозначались при помощи букв алфавита, над которыми ставились черточки: первые девять букв обозначали числа от 1 до 9, следующие девять - числа 10, 20, 30,..., 90, и следующие девять - числа 100, 200,..., 900. Таким образом, можно было обозначать любое число до 999.

Для обозначения чисел 1000, 2000,..., 9000 греки употребляли те же буквы, что и для чисел 1, 2,..., 9, но только при их записи ставили косую черточку слева внизу. Как это делалось, видно из прилагаемого здесь рисунка. Далее, для числа 10 000 употреблялся знак - это число называлось мириадой; две мириады, т. е. 20 000, обозначались так:. Этим способом можно было обозначить все числа до мириады мириад, т. е. до 108. Более высокие десятичные разряды уже не могли быть записаны в ионийской нумерации и не имели названия в древнегреческом языке.

Древние римляне пользовались нумерацией, которая сохраняется до настоящего времени под именем "римской нумерации". Мы пользуемся ею для обозначения юбилейных дат, для нумерации некоторых страниц книги (например, страниц предисловия), глав в книгах, строф в стихотворениях и т. д. В позднейшем своем виде римские цифры выглядят так:

I=1; V=5; X=10; L=50; С=100; D=500; M=1000.

Прежде они имели несколько иную форму. Так, число 1000 изображалось знаком (|), а 500-знаком |).

О происхождении римских цифр достоверных сведений нет. Цифра V могла первоначально служить изображением кисти руки, а цифра Х могла составиться из двух пятерок. Точно так же знак для 1000 мог составиться из удвоения знака для 500 (или наоборот).

В римской нумерации явственно сказываются следы пятеричной системы счисления. В языке же римлян (латинском) никаких следов пятеричной системы нет. Значит, эти цифры были заимствованы римлянами у другого народа (весьма вероятно у этрусков).

Все целые числа (до 5000) записываются с помощью повторения вышеприведенных цифр. При этом, если большая цифра стоит перед меньшей, то они складываются, если же меньшая стоит перед большей (в этом случае она не может повторяться), то меньшая вычитается из большей1). Например, VI=6, т.е. 5+1, IV=4, т.е. 5-1, XL=40, т е. 50-10, LX=60, т.е. 50+10. Подряд одна и та же цифра ставится не более трех раз: LXX=70; LXXX=80; число 90 записывается ХС (а не LXXXX).

Первые 12 чисел записываются в римских цифрах так:

I, II, III, IV, V, VI, VII, VIII. IX, X, XI, XII.

Примеры:

XXVIII=28; ХХХ1Х=39; CCCXCVII=397; MDCCCXVIII=1818.

Выполнение арифметических действий над многозначными числами в этой записи очень трудно. Тем не менее, римская нумерация преобладала в Италии до 13 века, а в других странах Западной Европы - до 16 века.

5.10. Наглядное представление перевода чисел

1. Из 2-ной системы в 8-ную (двоично-восьмеричное изображение):

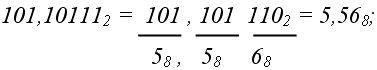
2. из 8-ной системы в 2–ную (восьмерично-двоичное изображение):

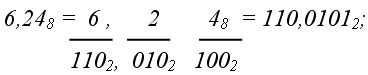
3. из 2-ной системы в 16-ную (двоично-шестнадцатеричное изображение):

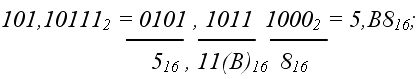
4. из 16-ной системы в 2-ную (шестнадцатерично-двоичное изображение):

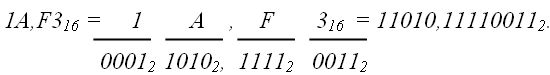
Дата добавления: 2014-01-06