Описание метода

МЕТОД НАИМЕНЬШИХ КВАДРАТОВ

Пусть в результате эксперимента получена таблица некоторой зависимости F(x)

Хi	X1	Х2	X3	…	Хn
F(x)	У1	У2	у3	…	Уn

Требуется найти функцию вида y=f(x), которая в точках x _1, x ₂, x _n принимает значения, наиболее близкие к табличным значениям У₁, У₂, •••, Уп.

Такую задачу называют задачей аппроксимации, формулу называют эмпирической формулой или уравнением регрессии у на х, а саму функцию называют приближаю­щей функцией.

На практике эту приближающую функцию F(x) находят следующим образом. По таблице строят точечный график функции F(x), по которому устанавливают вид приближающей функции из числа из­вестных..

Если вид приближающей функции установлен, то задача сводится к отысканию значений параметров. Их можно вычислить по методу наименьших квадратов, суть которого за­ключается в следующем.

Пусть требуется найти приближающую функцию, например с двумя параметрами:

у=F(х,а,Ь).

Для х_i, (где i = 1, 2,..., n) из таблицы эта функция примет значения 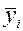= F(х, а,b), которые должны как можно меньше отличаться от заданных (табличных) значений у_i, т.е. разность 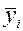- у_i, должна быть близка к нулю. Поэтому сумма квадратов разностей со­ответствующих значений функций ( 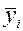- у_i),

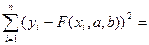Ф(a,b)

также должна принимать минимальное значение.

Таким образом, задачу свели к отысканию минимума функции Ф(а,b). Используем необходимое условие экстремума:

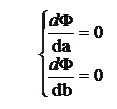Необходимый признак существования экстремума: если х = а является точкой экстремума функции y = f(x) и производная в этой точке существует, то она равна нулю: f'(a) = 0.

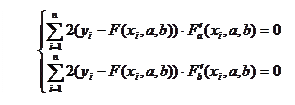
Решив эту систему из двух уравнений с двумя неизвестными, получим значения параметров а, b - следовательно, получим кон­кретный вид приближающей функции F(x, а, b).

Дата добавления: 2014-01-06