КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Коэффициент корреляции
|
|
|
|
Коэффициент корреляции показывает силу линейной зависимости между зависимой переменной х и независимой переменной у.
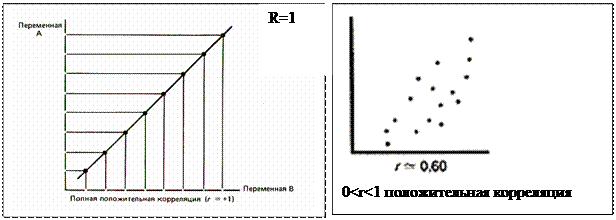
Наглядным изображением корреляционной таблице служит корреляционное поле. Оно представляет собой график, где на оси абсцисс откладывают значения Х, по оси ординат – У, а точками показывается сочетание Х и У. Получаем «облако» точек, по их концентрации в определенном направлении можно судить о наличии связи.
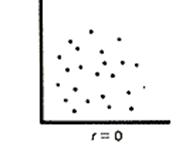
Коэффициент корреляции принимает значения в интервале от -1 до + 1.
 | |||||
|
| ||||
|
В случае если коэффициент корреляции равен 0, обе переменные полностью независимы друг от друга.
Коэффициент корреляции вычисляется по формуле:
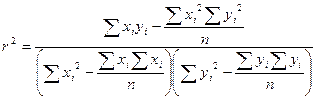
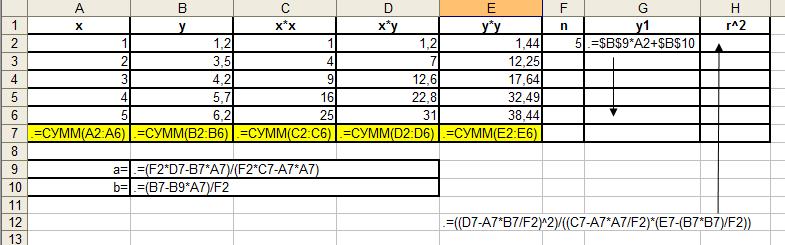
| 1.ЗАПОЛНИТЬ СТОЛБЕЦ Х И У, N ИСХОДНЫМИ ДАННЫМИ | ||||||||||||||
| 2.=А2^2 | ||||||||||||||
| 3. =A2*B2 | ||||||||||||||
| 4. НИЖЕ СТОЛБЦОВ С ДАННЫМИ ВЫЧИСЛИТЕ СУММЫ ПО СТОЛБЦАМ | ||||||||||||||
| 5. ВЫЧИСЛИТЬ А И В ПО ФОРМУЛАМ | ||||||||||||||
| 6. ВЫЧИСЛИТ У1 ПО ФОРМУЛЕ | ||||||||||||||
| 7. ВЫДЕЛИТЬ У И У1 И ПОСТРОИТЬ ДИАГРАММУ СРАВНЕНИЯ РЕЗУЛЬТАТОВ ВЫЧИСЛЕНИЯ(ТИП ГРАФИК) |
ВЫПОЛНИТЬ ПРОВЕРКУ
Выделяем столбец Х и У строим диаграмму точечную, затем меню Диаграмма –добавить линию Тренда– Параметры– показать уравнение на диаграмме _ добавить коэффициент аппроксимации.
Степенная функция (геометрическая регрессия)
Найдем теперь приближающую функция в виде:

Предполагая, что в исходной таблице значения аргумента и значения функции положительны, прологарифмируем равенство при условии а>0:
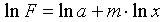
Так как функция F является приближающей для функции f, функция lnF будет приближающей для функции lnf. Введем новую переменную u=lnx; тогда, как следует из (12), lnF будет функцией от u: Ф(u).
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 420; Нарушение авторских прав?; Мы поможем в написании вашей работы!
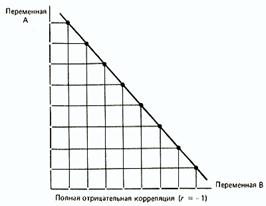
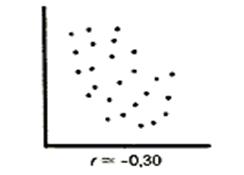 -1<r<0 отрицательная корреляция
-1<r<0 отрицательная корреляция