Вопрос 1. Тема 8. Выборочное наблюдение

Тема 8. Выборочное наблюдение.

План.

1. Выборочное наблюдение как основной вид несплошного наблюдения.

2. Обозначения показателей при выборочном наблюдении.

3. Способы отбора единиц; виды выборки.

4. Математические основы выборочного наблюдения (закон больших чисел).

5. Зависимость формул для оценки выборочного наблюдения от способов отбора.

6. Относительная ошибка выборки.

7. Малая выборка и ее особенности.

Первое выборочное наблюдение связано с именем Пьера Лапласа (1749–1827). В 1802 году выборочным методом была проведена перепись населения Франции. "Выборка охватила почти 7% общего числа жителей; затем на основе отношения числа жителей к числу рождений, приходящихся на переписанные общины, и данных об общем числе рождений в стране (по метрическим книгам) было исчислено население всей Франции с ошибкой, меньше полумиллиона."[1]

В 19 веке несплошные наблюдения (опросы населения) проводились в США, Германии, Бельгии, Англии, Норвегии. И, уже в 1903 году на Берлинской сессии Международного статистического института была принята резолюция о том, что выборка может дать точные результаты, если соблюдаются условия отбора наблюдаемых единиц.[2]

Выборочный метод применяется по двум основным причинам:

1) когда экономически не выгодно сплошное наблюдение;

2) когда наблюдение связано с уничтожением единиц наблюдения или невозможностью повторного исследования отобранных и обследованных единиц (анализ качественных характеристик продукции).

Первая причина проявляется тогда, когда сплошное наблюдение возможно, но его проведение требует больших затрат времени, человеческих ресурсов, финансово-материальных затрат, т.е. экономически невыгодно. Однако проведение правильно организованного выборочного наблюдения позволяет получить почти те же результаты, что и при сплошном наблюдении с определенной степенью достоверности (небольшой ошибкой).

Вторая причина в сельском хозяйстве возникает чаще всего там, где необходимо проанализировать качество кормов, молока, зерна или другой сельскохозяйственной продукции, при проведении контрольных доек коров, оценке предполагаемого урожая и др.

Выбор наблюдения проводится по следующей схеме:

1) определяют, какая часть совокупности подлежит выборочному наблюдению;

2) устанавливают правила отбора части совокупности;

3) производят отбор единиц совокупности;

4) определяют, как получить необходимые характеристики всей совокупности по результатам выборочного исследования.

Цель выборочного наблюдения – по результатам выборки оценить всю совокупность с определенной степенью точности.

Вопрос 2. При проведении выборочного наблюдения и оценке полученных результатов необходимо использовать некоторые понятия и определения.

Вся совокупность, из которой производят отбор, называется генеральной совокупностью.

N – численность генеральной совокупности или ее объем,

– среднее значение анализируемого признака в генеральной совокупности.

Часть генеральной совокупности, попавшая в выборку, называется выборочной совокупностью или выборкой.

n – численность выборочной совокупности и ее объем,

– среднее значение анализируемого признака в выборочной совокупности.

Силу вариации анализируемого признака оценивают по значениям дисперсии:

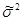– дисперсия генеральной совокупности,

– дисперсия выборочной совокупности.

Когда необходимо оценить у единиц генеральной и выборочной совокупностей наличие какого-либо признака, то проводят оценку доли выборки и доли генеральной совокупности

- доля генеральной совокупности,

ω – доля выборочной совокупности

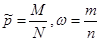, где

"M" и "m" – число единиц в генеральной и выборочной совокупностях соответственно, обладающих анализируемым признаком.

Долей называется та часть генеральной или выборочной совокупности, которая обладает определенным признаком.

Отклонение значения характеристики выборочного наблюдения от характеристики генерального совокупности называется ее ошибкой.

- ошибка репрезентативности выборочной средней,

- ошибка частности или доли,

- ошибка дисперсии.

Чем меньше эти ошибки, тем лучше выборочная совокупность характеризует совокупность генеральную.

При проведении выборочного наблюдения возникает ряд вопросов или проблем, связанных с точностью проводимого обследования:

Сколько может быть выборочных средних? Сколькими способами можно отобрать единицы в выборку "n" из генеральной совкупности "N"? Какова должна быть величина выборки "n"? Как нужно отбирать единицы в выборочную совокупность? От чего зависит точность проводимого исследования?

Эти другие вопросы рассмотрим ниже.

Вопрос 3.

При выборочном исследовании различают способы отбора единиц и виды выборки.

Под способом отбора понимают порядок отбора единиц из генеральной совокупности в выборочную.

Дата добавления: 2014-01-06