Линейная деформация

Деформация и вращение жидкой частицы

Динамика вязкой жидкости

Области живота.

Границы:

- верхняя – проекция диафрагмы

- нижняя – лобковый симфиз

Сначала три отдела делятся горизонтальными линиями:

1. Надчревье (эпигатсриум)

2. Чревье (мезогастриум)

3. Подчревье (гипогастриум)

Далее три области разделяются еще на три – по наружному краю прямой мышцы живота с обеих сторон.

Итого 9 оластей:

I. 1,2 – правая и левая подреберные области, 3 – эпигастральная область

II. 4,5 – правая и левая боковые области живота, 6 – пупочная область

III. 7,8 – правая и левая паховые области, 9 – лобковая область.

В общем случае движение жидкой частицы является весьма сложным. При этом имеет место три типа движения:

1. Поступательное движение.

2. Вращение частицы относительно собственных осей

3. Деформационное движение

Что касается деформации, то в случае движения жидкой частицы имеет место:

- линейная деформация (удлинение, сжатие частицы);

- угловая деформация (деформация сдвига, скашивания).

Рассмотрим линейную деформацию

Для простоты рассмотрим плоскопараллельное движение жидкой частицы. Выделим частицу жидкости в виде элементарного параллелепипеда.

Как очевидно, растяжение отрезка dx происходит вследствие разности скоростей в точках О и А. Если бы скорости в этих точках были одинаковыми, то отрезок dx двигался бы поступательно без расширения или сжатия. Пусть в точке О x–овая составляющая скорости равная 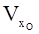. Тогда для точки А, находящейся в окрестности точки О, можно записать

(7.1)

Приведенная запись отвечает разложению в ряд Тейлора при ограничении линейным членом ввиду малости отрезка dx.

Точка О за время 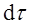пройдет расстояние 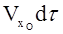, а точка А соответственно

.

Изменение длины элемента dxсоставит

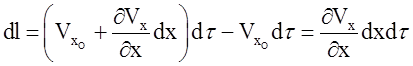
Тогда изменение длины элемента dxв единицу времени (или, что тоже самое, скорость его удлинения) равно

.

Скорость же относительного удлинения элемента, т.е. скорость удлинения, отнесенная к первоначальной длине элемента dx, составит

.

В литературе данная величина называется также скоростью относительной линейной деформации вдоль оси x и обозначается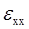

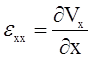
Аналогично вводятся величины скорости относительной линейной деформации по координатам y, z:

, .

Легко доказать, что справедливо следующее равенство.

, (7.2)

где υ - объем частицы.

Данное равенство выражает следующее утверждение:

	В любой точке жидкости относительное изменение удельного объема в единицу времени, равно сумме скоростей относительных линейных деформаций по любым трем взаимно-перпендикулярным направлениям.

Дата добавления: 2014-01-06