Президент Фарадеевского общества (1948-1950 гг.)

Джон-Эдвард ЛЕННАРД-ДЖОНС (Lennard-Jones J.A.)

(27.X. 1894 - 1.XI. 1954)

Джон-Эдвард Леннард-Джонс - английский химик-теоретик, член Лондонского королевского общества (с 1933 г.). Родился в Ли (Ланкашир). Окончил Манчестерский университет (1915 г.). В 1915-1919 гг. служил в Королевских военно-воздушных силах. С 1919 г. преподавал в Манчестерском и Кембриджском университетах, в 1925-1932 гг. - в Бристольском университете (с 1927 г. - профессор). В 1929 г. изучал квантовую механику в Гёттингенском университете. В 1932-1953 гг. преподавал в Кембриджском университете, с 1953 г. - в Университетском колледже Северного Стаффордшира.

Работы посвящены преимущественно квантовой химии. Один из создателей (наравне с Ф. Хундом и Р.-С. Малликеном; 1928-1932 гг.) одного из методов квантовой химии - метода молекулярных орбиталей. Положил начало широкому применению этого метода к расчетам органических соединений с сопряженными связями (1937 г.) и к системам с сигма-электронами (1949 г.). Развивал квантово-механические методы применительно к неорганическим объектам.

Леннард-Джонс впервые теоретически обосновал (1932 г.) возможность образования ковалентной связи между поверхностью адсорбента и атомом адсорбата. Показал, что величина энергии активации образования такой связи является критерием типа адсорбции (химический или физический). Развил идеи об энергетической неоднородности поверхности, содержащей "потенциальные долины", по которым молекула адсорбента может перемещаться без хемосорбции.

Массу удобно выражать в безразмерных единицах. В нашем случае примем массу частиц за единицу какой-либо массы, m=1, например единица массы может быть равна массе молекулы вещества, поведение которого моделируем.

Время также удобно выражать в безразмерных единицах (хотя при программировании можно оставлять его в сек, нанаосек, пикосек и т.д.). Рассмотрим это подробно. Оставаясь в рамках рассмотренной физической модели, будем считать, что частица, находящаяся в потенциале Леннарда-Джонса, при малых смещениях от точки минимума будет совершать линейные гармонические колебания с периодом Т, который мы вычислим. Эту величину будем использовать для обезразмеривания времени ().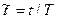

Рассмотрим уравнение гармонических колебаний:

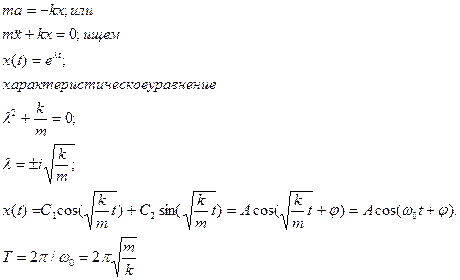
ω₀ – циклическая, или круговая, частота колебаний, T – период колебаний гармонического маятника. Сравним его с периодом колебаний частицы в потенциале Леннарда-Джонса. Разложим потенциал

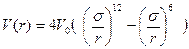в ряд Тейлора вблизи минимума потенциала (r₀=2^1/6 σ). Сохранив члены ряда, пропорциональные первой и второй производной и приведя подобные^*, получим:

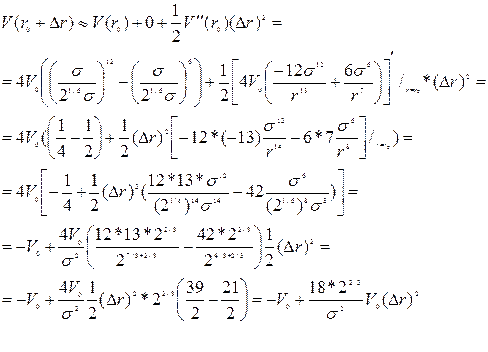
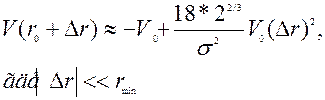
Сравним выражение для V(Δr) c известным выражением для потенциальной энергии гармонического осциллятора 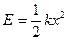, можно считать, что величина 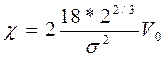является аналогом коэффициента жесткости пружины гармонического осциллятора, которым можно моделировать малые колебания частицы. Т.е. частица, находящаяся в потенциале Леннарда-Джонса, при малых смещениях от точки минимума будет совершать линейные гармонические колебания с периодом 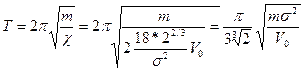. Можно коэффициент перед корнем учесть потом, после всех расчетов. Например, для жидкого аргона V₀/k_b=119,8 K (постоянная Больцмана k_b=1,38*10^-16 эрг/град), σ=3,405*10^-8см, масса атома аргона m=6,69*10^-23г, Т=0,831*0,216*10^-11=1,79*10^-12сек.

Рассмотрим математическую модель.

Перепишем СДУ в виде:

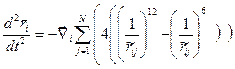, i=1…N, где 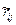=││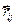=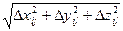, вектор 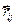имеет координаты (x_i –x_j, y_i-y_j, z_i-z_j)=(Δx_ij,Δy_ij,Δz_ij). В СДУ N векторных уравнений или 3N скалярных (для трехмерного случая) и 2N скалярных (для двумерного случая). Перепишем систему в скалярном виде, учтем, что m=1, и найдем выражение правых частей уравнений через координаты.

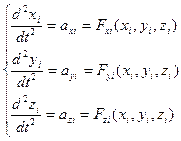, i=1…N

Рассмотрим только пары частиц, i-я частица взаимодействует с остальными N-1 частицами. Тогда потенциальная энергия взаимодействия двух частиц (опустим нижние индексы у и т.д.) имеет вид

.

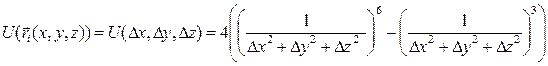Найдем проекции сил взаимодействия пар частиц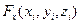, 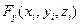и 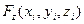, как проекции (-gradU) на оси 0x, 0y, 0z.

Т.о. 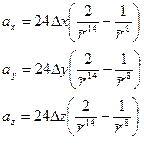и в СДУ будут суммы по всем парам частиц, она имеет вид, пригодный для решения

Вернем индексы для приращения координат i-ой частицы и просуммируем все силы со стороны всех остальных частиц, действующих на нее:

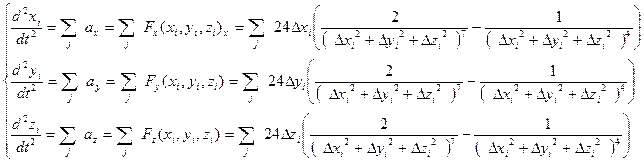
Если взаимодействуют две частицы, i-я и j-я, то в силу третьего закона Ньютона, если на i-ю частицу со стороны j-ой действует сила 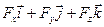, то на j-ю со стороны i-ой действует сила –().

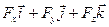Рассматривая попарные взаимодействия, учтем изменения координат и скоростей всех частиц, чтобы в любой момент времени знать все скорости и координаты каждой частицы. Чтобы избежать повторного вычисления силы взаимодействия частиц, можно фиксировать номер частицы от i до N (эта частица движется, получает мгновенное приращение координат, скорости и т.д.), а остальные частицы с номерами j (j меняется от i+1 до N) действуют на нее, оставаясь как бы в стационарном состоянии.

Дата добавления: 2014-01-06