Показатели рядов динамики и методы их исчисления

Средняя гармоничная простая

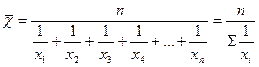
-рассмотрение рядов динамики (временных рядов)

Динамический ряд - это статистические показатели, которые расположены в хронологической последовательности и характеризуют развитие того или другого социально-экономического явления во времени.

Последовательность уровней можно записать так:

Х1, Х2, Х3, … Хп

где Х - число уровней (длина динамического ряда).

За признаком времени динамические ряды разделяют на моментные и периодические (интервальные).

Абсолютный прирост (АП_n) отображает абсолютную скорость изменения уровней ряда за определенный интервал времени.

Темп роста или коэффициент роста (ТР_n) характеризует интенсивность изменения уровней ряда.

Темп прироста (ТП_n) - это соотношение абсолютного прироста и базового уровня.

Абсолютное значение 1% прироста (А_n) дает представление о весомости одного процента прироста и определяется как часть от деления абсолютного прироста на темп прироста. Если скорость развития в пределах периода, который изучается, неодинаковая, сравнением одноименных характеристик скорости измеряется ускорение или замедление динамики.

Абсолютное ускорение - это разность между абсолютными приростами: Δn=АП–АП_n-1. Ускорение характеризуется положительной величиной, а замедление - отрицательной.

Темп роста абсолютной скорости исчисляется как соотношение абсолютных приростов (исчисляется только на основании додатних абсолютных приростов).

В статистическом анализе сравнивается также интенсивность динамики в разных рядах. Отношение темпов роста ТЗ^//: ТЗ^/ называют коэффициентом опережения.

Относительно темпов прироста соотношение используют лишь для взаимосвязанных показателей х і у. Такое соотношение называют коэффициентом эластичности:

К=ТП_У:ТП_Х

Он показывает, на сколько процентов изменяется в с изменением х на один процент.

3.3 Математико-статистичні методи вивчення зв'язків

Метод кореляційно-регрессивного анализа

Метод кореляційно-регрессивного анализа широко используется для определения тесноты связи между показателями, которые не находятся в функциональной зависимости. Плотность связи между изучаемыми явлениями измеряется корреляционным отношением (для криволинейной зависимости). Для прямолинейной зависимости вычисляется коэффициент корреляции.

Корреляционный анализ – применяется для исследования стохастических, вероятностных зависимостей между признаком-фактором и признаком –результатом. Данные для корреляционного анализа могут быть получены либо с одного предприятия за определенные промежутки времени либо с однородных объектов в один и тот же момент времени.

Корреляционный анализ направлен на решение 2 задач:

- Установление связи между параметрами

- Оценка тесноты связи

Если исследуются 2 переменные говорят о парной корреляции, если система переменных - о многомерной корреляции.

Алгоритм:

1 шаг Определяем степень тесноты связи между рассматриваемыми показателями.

Цель установить существование самой связи и ее вид: прямая-обратная. Для этого используется коэффицинт корреляции. Он лежит в окресности 1. чем ближе к 1, тем теснее связь.

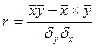
Как известно,

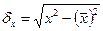
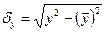
Шаг 2. Определяем коэффициент детерминации – чтобы количесивенно оцеить тесноту связи

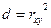
Шаг 3. строим уравнение регресии, для чего решаем систему нормальных уравнений

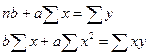или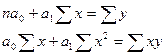

Шаг 4. находим ошибку аппроксимации, чтоб определить насколько модель адекватна. Ведь мы взяли линейную функцию, а могла быть парабола, гипербола и т.д.

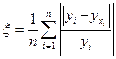
Где теоретическое значение результирующего показателя при каждом значении х

Методы линейного программирования

Методы линейного программирования применяются для решения многих экстремальных задач, с которыми довольно часто приходится иметь дело в экономике. Решение таких задач сводится к нахождению крайних значений (максимума и минимума) некоторых функций переменных величин.

Линейное программирование основано на решении системы линейных уравнений (с преобразованием в уравнения и неравенства), когда зависимость между изучаемыми явлениями строго функциональна.

Как пример рассмотрим решение задачи рациональности использования времени работы производственного оборудования.

Согласно оперативного плана участок шлифования за первую неделю декабря выпустила 500 колец для подшипников типа А, 300 колец для подшипников типа Б и 450 колец для подшипников типа В. Все кольца шлифовались на двух взаимозаменяемых деталей различной производительности. Машинное время каждого станка составляет 5 000 мин. Трудоемкость операций (в минутах на одно кольцо) при изготовлении различных колец характеризуется следующими данными (табл. 1.9).

Таблица - Трудоемкость операций при изготовлении колец

Верстати	Витрати часу на одне кільце типів, хв.
А	Б	В
I
II

Следует определить оптимальный вариант распределения операций за станками и временем, которое было бы потрачено при этом оптимальном варианте. Задачу выполняем с помощью симплексного метода.

Для составления математической модели данной задачи введем следующие условные обозначения:

х₁, х₂, х₃, – відповідно кількість кілець для підшипників типів А, Б, В, вироблених на верстаті I;

х₄, х₅, х₆, – відповідно кількість кілець для підшипників типів А, Б, В, вироблених на верстаті П.

Линейная форма, отражающая критерий оптимальности, будет иметь такой вид

min a(x) = 4x₁ + 10x₂ + 10x₃ + 6x₄ + 8x₅ + 20x₆ (3.1)

при обмеженнях

4x₁ + 10x₂ + 10x₃ £ 5000

6x₄ + 8x₅ + 20x₆ £ 5000

x₁ +x₄ = 500

x₂ + x₅ = 300

x₃ +x₆ = 450

x_j ³ 0, j = 1,..., 6

Изменим условие задачи введением дополнительных (вспомогательных) и фиктивных переменных. Запишем так:

min a(x) = 4x₁ + 10x₂ + 10x₃ + 6x₄ + 8x₅ + 20x₆ + Mx₉ + Mx₁₀ + Mx₁₁ (3.2)

Система уравнений, что отражает ограничительные условия машинного времени и количество произведенной продукции:

4x₁ + 10x₂ + 10x₃ + х₇ £ 5000

6x₄ + 8x₅ + 20x₆ + х₈ £ 5000

x₁ +x₄ х₉ = 500

x₂ +x₅ х₁₀ = 300

x₃ +x₆ х₁₁ = 450

x_j ³ 0, j = 1,..., 11

Оптимальный вариант полученный на седьмом этапе (итерации). Если бы на станке І производилось 125 колец подшипников типа А, 450 колец подшипников типа В, на станке II - 375 колец подшипников типа А и 300 колец подшипников типа Б, то при такой загрузке оборудования были бы освобождены 350 минут машинного времени станка II. Общие затраты времени по оптимальным вариантом составили бы 9 650 мин., тогда как фактически потрачены 10 000 минут машинного времени.

Кластерный анализ

Кластерный анализ - один из методов многомерного анализа, предназначенный для группировки (кластеризации) совокупности, элементы которой характеризуются многими признаками.

Дисперсионный анализ

Дисперсионный анализ-позволяет подтвердить или опровергнуть гипотезу о том, что две выборки данных относятся к одной главной совокупности. Относительно анализа деятельности предприятия можно сказать, что дисперсионный анализ позволяет определить, или к одной и той же совокупности, а или к разным относятся группы наблюдений.

Дисперсионный анализ часто используется вместе с методами группировки. Задача его проводки в этих случаях составляется в оценке существенности расхождений между группами.

Дата добавления: 2014-01-06