О конечности симплекс - метода

Пусть ЗЛП является невырожденной. Тогда на каждом шаге симплекс – метода будем иметь . Процесс расчета будет состоять в переходе

,

где два соседних базиса отличаются лишь одним вектором. Например, переход от 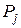к 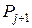осуществлен введением вектора 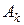. При этом линейная форма изменится так:

,

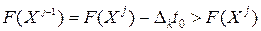т.к. и .

Таким образом, при переходе от одного опорного плана к другому в невырожденной задаче линейная форма возрастает. Поэтому невозможен возврат к старому опорному плану, т.е. каждый шаг симплекс – метода приводит к новому, ранее не встречавшемуся, опорному плану. И поскольку число опорных планов (вершин многогранного множества 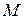) конечно, то в невырожденной задаче через конечное число шагов либо устанавливается неограниченность линейной формы, либо получается оптимальный план.

Пусть ЗЛП является вырожденной. Тогда у вырожденного опорного плана может быть (но не обязательно) и поэтому может быть .

Не приведет ли это к бесконечному числу шагов? В силу конечности числа вершин множества 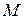это может быть лишь тогда, когда через несколько шагов мы вернемся к исходному базису. Следовательно, должны встречаться цепочки

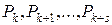
в которых начальное и конечное звенья совпадают, т.е. . Такие цепочки называются циклами. Для них 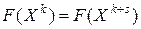. Но так как любые соседние опорные планы доставляют значение линейной формы , то, очевидно,

.

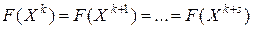Таким образом, цикл означает переход от одного базиса опорного плана к другому базису того же вырожденного опорного плана. Причем, через некоторое число таких переходов имеет место возвращение к ранее встретившемуся базису. В случае образования цикла, т.е. зацикливания, всегда можно выйти из него, специальным образом выбрав «разрешающий элемент».

Дата добавления: 2014-01-06