
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Элементы выпуклого анализа
|
|
|
|
Приведем некоторые определения и рассмотрим конкретные примеры выпуклых множеств. Мы будем в дальнейшем иметь дело с функциями, определенными на множествах конечномерного евклидова пространства En.
Определение 12.1. Множество  вида
вида
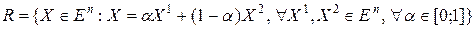 (12.2)
(12.2)
называется отрезком, соединяющим точки  и
и 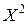 , и обозначаемым
, и обозначаемым 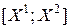 .
.
Очевидно, при  точка X совпадет с одним из концов отрезка (
точка X совпадет с одним из концов отрезка (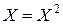 ), при
), при  – с другим (
– с другим ( ), а при
), а при 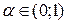 - с некоторой внутренней точкой отрезка.
- с некоторой внутренней точкой отрезка.
Определение 12.2. Множество  называется выпуклым, если вместе с любыми двумя точками
называется выпуклым, если вместе с любыми двумя точками  и
и  ему принадлежит и отрезок
ему принадлежит и отрезок 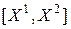 их соединяющий.
их соединяющий.
Выпуклость множества  означает, что из принадлежности
означает, что из принадлежности  и
и 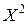 множеству
множеству  следует, что
следует, что 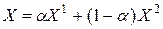 принадлежит
принадлежит  для всех
для всех  .
.
Очевидно, в  выпуклы отрезок, полупрямая, прямая, круг, треугольник, полуплоскость и вся плоскость.
выпуклы отрезок, полупрямая, прямая, круг, треугольник, полуплоскость и вся плоскость.
Все пространство 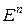 , очевидно, образует выпуклое множество. Пустое множество и множество, состоящее из одной точки, удобно считать выпуклыми.
, очевидно, образует выпуклое множество. Пустое множество и множество, состоящее из одной точки, удобно считать выпуклыми.
Теорема 12.1. Теорема Фаркаша. Пусть заданы матрица 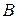 размерности
размерности 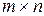 и вектор
и вектор 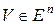 . Неравенство
. Неравенство 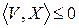 выполняется для всех
выполняется для всех  в том и только том случае, если существует вектор
в том и только том случае, если существует вектор 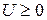 такой, что
такой, что  .
.
Д о к а з а т е л ь с т в о. Достаточность. Пусть выполняются соотношения 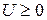 и
и  . Тогда для любого вектора
. Тогда для любого вектора  будет
будет
 .
.
Необходимость. Пусть для всех  справедливо
справедливо 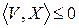 . Рассмотрим конус
. Рассмотрим конус  . Если
. Если 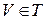 , то теорема доказана. Предположим, что
, то теорема доказана. Предположим, что  . Множество
. Множество 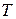 , по определению 12.2, выпукло и замкнуто, поэтому в силу теоремы отделимости существует вектор
, по определению 12.2, выпукло и замкнуто, поэтому в силу теоремы отделимости существует вектор 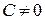 такой, что
такой, что
 (12.3)
(12.3)
для всех 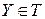 .
.
Так как 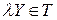 при всех
при всех 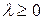 , то из (12.3) получаем, что
, то из (12.3) получаем, что 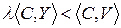 при всех
при всех 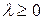 . Значит
. Значит  . С другой стороны
. С другой стороны 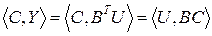 . То есть
. То есть  и так как это имеет место для всех
и так как это имеет место для всех 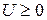 , то
, то
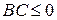 . (12.4)
. (12.4)
Но 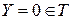 , поэтому из (12.3) следует
, поэтому из (12.3) следует
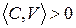 . (12.5)
. (12.5)
Взяв  , из (12.4) и (12.5) получаем противоречие условиям теоремы.
, из (12.4) и (12.5) получаем противоречие условиям теоремы.
Замечание. Приведем геометрическое истолкование теоремы Фаркаша. Пусть
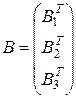
и 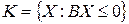 . Конус
. Конус  есть совокупность всех векторов
есть совокупность всех векторов 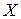 , которые образуют с каждым из векторов
, которые образуют с каждым из векторов 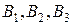 неострые углы. На рис 12.1 конус
неострые углы. На рис 12.1 конус  заштрихован вертикальными линиями, а конус
заштрихован вертикальными линиями, а конус  - горизонтальными. Геометрический смысл теоремы таков. Чтобы для любого вектора
- горизонтальными. Геометрический смысл теоремы таков. Чтобы для любого вектора  угол между
угол между 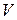 и
и 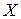 был неострым, необходимо и достаточно, чтобы
был неострым, необходимо и достаточно, чтобы 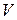 принадлежал конусу
принадлежал конусу 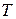 .
.

Рис 12.1
Определение 12.3. Функция 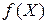 , заданная на выпуклом множестве
, заданная на выпуклом множестве  , называется выпуклой, если для любых точек
, называется выпуклой, если для любых точек 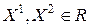 и любого
и любого  выполняется неравенство
выполняется неравенство
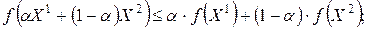 (12.6)
(12.6)
Функция 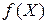 называется строго выпуклой, если для всех
называется строго выпуклой, если для всех 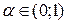 неравенство (12.6) выполняется как строгое. Функция называется сильно выпуклой, если существует такое число,
неравенство (12.6) выполняется как строгое. Функция называется сильно выпуклой, если существует такое число, 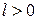 (константа сильной выпуклости), что для всех
(константа сильной выпуклости), что для всех 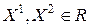 и любого
и любого  выполняется неравенство
выполняется неравенство
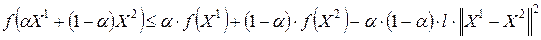 (12.7)
(12.7)
Всякая сильно выпуклая функция является строго выпуклой и тем более выпуклой функцией, но не наоборот.
Примером выпуклой функции служит квадратичная функция с положительно определенной матрицей.
Теорема 12.2. Линейная комбинация с неотрицательными коэффициентами выпуклых на выпуклом множестве функций есть выпуклая функция на данном множестве.
Д о к а з а т е л ь с т в о. Пусть функции 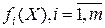 , определенные на выпуклом множестве
, определенные на выпуклом множестве  , является выпуклым на
, является выпуклым на  . Покажем, что функция
. Покажем, что функция
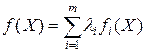 , (12.8)
, (12.8)
где 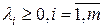 выпукла на
выпукла на  .
.
Для произвольных точек  и
и 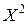 из
из  и любого числа
и любого числа  имеем
имеем
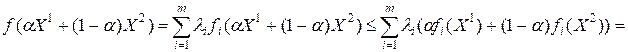
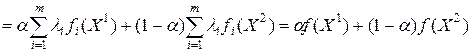 .
.
В этой цепочке соотношений первое неравенство справедливо, поскольку функции  выпуклые. Полученный результат показывает, что функция
выпуклые. Полученный результат показывает, что функция 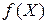 , определяемая формулой (12.8) является выпуклой на множестве
, определяемая формулой (12.8) является выпуклой на множестве  .
.
Теорема 12.3. Если 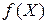 выпукла на выпуклом множестве
выпукла на выпуклом множестве  , то для любых точек
, то для любых точек 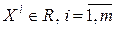 и любых чисел
и любых чисел  , таких что
, таких что  выполняется неравенство Йенсена
выполняется неравенство Йенсена
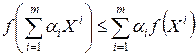 . (12.9)
. (12.9)
Д о к а з а т е л ь с т в о (по индукции). При 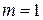 неравенство (12.9) очевидно. В самом деле, если
неравенство (12.9) очевидно. В самом деле, если 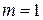 , то
, то 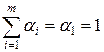 и
и 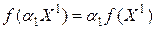 , т.е. (12.9) выполняется как равенство. Предположим, что (12.9) имеет место для
, т.е. (12.9) выполняется как равенство. Предположим, что (12.9) имеет место для 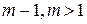 , т.е. для выпуклой комбинации из
, т.е. для выпуклой комбинации из 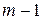 точек. Покажем, что тогда оно справедливо и для выпуклой комбинации из
точек. Покажем, что тогда оно справедливо и для выпуклой комбинации из  точек множества
точек множества  , т.е.
, т.е.
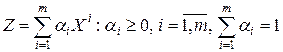 ,
,
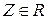 . При этом, если
. При этом, если  , то
, то  и в (12.9) очевидно равенство. Если же
и в (12.9) очевидно равенство. Если же 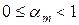 . То из выпуклости
. То из выпуклости 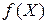 и индуктивного предположения следует
и индуктивного предположения следует
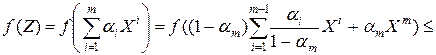

 .
.
Говорят, что множество 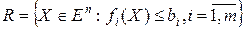 удовлетворяет условию регулярности, если для каждого
удовлетворяет условию регулярности, если для каждого 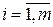 существует точка
существует точка  такая, что
такая, что  , т.е.
, т.е.
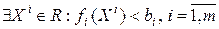 (12.10)
(12.10)
Нетрудно показать, что условию (12.10) эквивалентно другое условие, называемое условием регулярности Слейтера.
Теорема 12.4. Если для множества 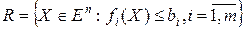 выполняется условие регулярности (12.10), то множество
выполняется условие регулярности (12.10), то множество  регулярно по Слейтеру, а именно существует точка
регулярно по Слейтеру, а именно существует точка 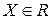 , в которой все ограничения выполняются строго
, в которой все ограничения выполняются строго
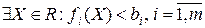 . (12.11)
. (12.11)
Д о к а з а т е л ь с т в о. Пусть выполняется условие регулярности (12.10). Выберем точку 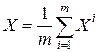 , являющуюся выпуклой комбинацией точек
, являющуюся выпуклой комбинацией точек 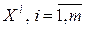 и, следовательно, принадлежащую
и, следовательно, принадлежащую  . Тогда при любом
. Тогда при любом 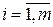 будем иметь
будем иметь

 .
.
т.е. 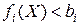 . В этой цепочке соотношений первое неравенство справедливо в силу неравенства Йенсена, а второе – поскольку, по крайней мере, один член суммы, а именно
. В этой цепочке соотношений первое неравенство справедливо в силу неравенства Йенсена, а второе – поскольку, по крайней мере, один член суммы, а именно  строго меньше
строго меньше  . Эти неравенства показывают, что для рассматриваемого
. Эти неравенства показывают, что для рассматриваемого  имеет место условие регулярности Слейтера.
имеет место условие регулярности Слейтера.
Приведем без доказательства следующее важное свойство выпуклых функций.
Выпуклая функция 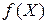 , определенная на выпуклом множестве
, определенная на выпуклом множестве  непрерывна в каждой внутренней точке этого множества и имеет в каждой внутренней точке производную по любому направлению
непрерывна в каждой внутренней точке этого множества и имеет в каждой внутренней точке производную по любому направлению 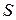
 .
.
Важное свойство выпуклых дифференцируемых функций, которым мы будем часто пользоваться, устанавливает следующая теорема.
Теорема 12.5. Функция 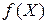 , дифференцируемая на выпуклом множестве
, дифференцируемая на выпуклом множестве  , выпукла тогда и только тогда, когда для любых
, выпукла тогда и только тогда, когда для любых  и
и 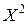 , принадлежащих
, принадлежащих  выполняется неравенство
выполняется неравенство
 . (12.12)
. (12.12)
Д о к а з а т е л ь с т в о. Необходимость. Пусть 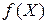 выпукла. Тогда для любых
выпукла. Тогда для любых 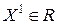 и
и  , (
, ( ) и всех
) и всех 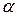 таких, что
таких, что  справедливо неравенство
справедливо неравенство
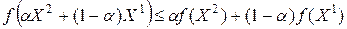
или
 ,
,
откуда
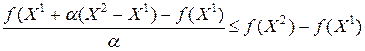
Переходя к пределу в последнем неравенстве при  , получим
, получим
 .
.
Достаточность. Пусть теперь выполняется условие (12.12) для любых двух точек множества  . Тогда для точки
. Тогда для точки 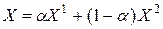 при
при  , принадлежащей
, принадлежащей  , справедливы неравенства
, справедливы неравенства
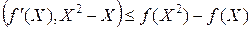 и
и  .
.
Умножив первое неравенство на 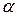 , второе - на
, второе - на  и сложив полученные неравенства, имеем
и сложив полученные неравенства, имеем

или, учитывая, что 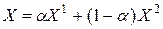 имеем
имеем
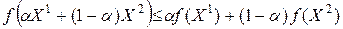 ,
,
т.е, что 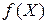 выпуклая функция на множестве
выпуклая функция на множестве  .
.
Рассмотрим ряд экстремальных свойств выпуклых функций на выпуклом множестве, играющих существенную роль при решении задачи отыскания точки  выпуклого множества
выпуклого множества  , в которой выпуклая функция
, в которой выпуклая функция 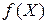 , определенная на
, определенная на  достигает минимального значения:
достигает минимального значения:  .
.
Теорема 12.6. Любая точка локального минимума функции 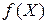 на выпуклом множестве
на выпуклом множестве  является точкой глобального минимума
является точкой глобального минимума
Д о к а з а т е л ь с т в о. Пусть  - точка локального минимума функции
- точка локального минимума функции 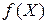 на
на  . Тогда по определению точки локального минимума существует некоторая окрестность
. Тогда по определению точки локального минимума существует некоторая окрестность  этой точки такая, что выполняется неравенство
этой точки такая, что выполняется неравенство
 . (12.13)
. (12.13)
Предположим, что  не является точкой глобального минимума функции
не является точкой глобального минимума функции 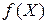 , то есть что существует точка
, то есть что существует точка 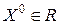 такая, что
такая, что  . Рассмотрим точки вида
. Рассмотрим точки вида 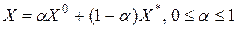 .
.
Так как множество  выпукло, то
выпукло, то 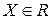 . Далее из выпуклости
. Далее из выпуклости 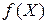 и из предположения о
и из предположения о  следует
следует
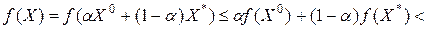
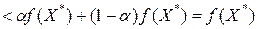 .
.
т.е. 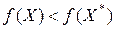 . Но это противоречит условию, что
. Но это противоречит условию, что  - точка локального минимума, поскольку при достаточно малых
- точка локального минимума, поскольку при достаточно малых 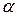 точка
точка 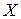 находится в окрестности
находится в окрестности  , где имеет место (12.13).
, где имеет место (12.13).
Следовательно,  - точка глобального минимума
- точка глобального минимума 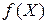 на
на  .
.
Теорема 12.7. Множество точек минимума выпуклой функции на выпуклом множестве является выпуклым множеством.
Д о к а з а т е л ь с т в о. Пусть  - множество точек минимума выпуклой функции
- множество точек минимума выпуклой функции 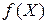 на выпуклом множестве
на выпуклом множестве  , т.е.
, т.е.
 .
.
Выберем две любые точки  и
и 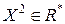 . Поскольку
. Поскольку  и
и  - выпуклое множество, то для любого
- выпуклое множество, то для любого  будет
будет
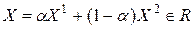 ,
,
а ввиду выпуклости функции 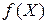 имеем
имеем

То есть  . Кроме того, поскольку
. Кроме того, поскольку  - минимальное значение функции
- минимальное значение функции 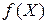 на
на  , то
, то 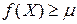 . А, значит,
. А, значит,  , т.е.
, т.е. 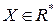 . Следовательно,
. Следовательно,  - выпуклое множество.
- выпуклое множество.
Теорема 12.8. Строго выпуклая функция на выпуклом множестве достигает своего минимума не более чем в одной точке.
Д о к а з а т е л ь с т в о. Пусть 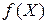 - строго выпуклая функция на выпуклом множестве
- строго выпуклая функция на выпуклом множестве  , т.е. для любых
, т.е. для любых 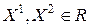 и всех
и всех  выполнятся строгое неравенство
выполнятся строгое неравенство
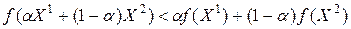 .
.
Пусть  =
=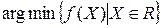 .
.
Предположим, что найдется точка 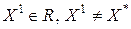 , такая, что
, такая, что
 .
.
Тогда для любого 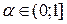 точка
точка 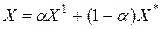 принадлежит множеству
принадлежит множеству  и в силу строгой выпуклости функции
и в силу строгой выпуклости функции 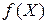 будет
будет
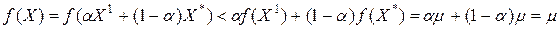
т.е.  . Это противоречит условию, что
. Это противоречит условию, что  - точка минимума. Следовательно, точка
- точка минимума. Следовательно, точка  единственна.
единственна.
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 1095; Нарушение авторских прав?; Мы поможем в написании вашей работы!