Равносильные преобразования. Упрощение формул

Если в равносильные формулы всюду вместо какой-нибудь переменной подставить одну и ту же формулу, то вновь полученные формулы также окажутся равносильными в соответствии с правилом подстановки. Таким способом из каждой равносильности можно получить сколько угодно новых равносильностей.

Пример 1: Если в законе де Моргана вместо Х подставить , а вместо Y подставить , то получим новую равносильность . Справедливость полученной равносильности легко проверить с помощью таблицы истинности.

Если какую-нибудь формулу , являющуюся частью формулы F, заменить формулой , равносильной формуле , то полученная формула окажется равносильной формуле F.

Тогда для формулы из примера 2 можно провести следующие замены:

– закон двойного отрицания;

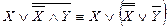– закон де Моргана;

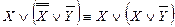– закон двойного отрицания;

– закон ассоциативности;

– закон идемпотентности.

По свойству транзитивности отношения равносильности можем утверждать, что .

Замену одной формулы другой, ей равносильной, называют равносильным преобразованием формулы.

Под упрощением формулы, не содержащей знаков импликации и эквиваленции, понимают равносильное преобразование, приводящее к формуле, которая не содержит отрицаний неэлементарных формул (в частности, двойных отрицаний) или содержит в совокупности меньшее число знаков конъюнкции и дизъюнкции, чем исходная.

Пример 2: Упростим формулу .

.

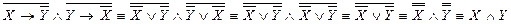На первом шаге мы применили закон, преобразующий импликацию в дизъюнкцию. На втором шаге применили коммутативный закон. На третьем шаге применили закон идемпотентности. На четвертом – закон де Моргана. И на пятом – закон двойного отрицания.

Замечание 1. Если некоторая формула является тавтологией, то и всякая равносильная ей формула также является тавтологией.

Таким образом, равносильные преобразования можно также применять для доказательства тождественной истинности тех или иных формул. Для этого данную формулу нужно равносильными преобразованиями привести к одной из формул, которые являются тавтологиями.

Замечание 2. Некоторые тавтологии и равносильности объединены в пары (закон противоречия и закон альтернативы, коммутативный, ассоциативный законы и т.д.). В этих соответствиях проявляется так называемый принцип двойственности.

Две формулы, не содержащие знаков импликации и эквиваленции, называются двойственными, если каждую из них можно получить из другой заменой знаков соответственно на .

Принцип двойственности утверждает следующее:

Теорема 2.2: Если две формулы, не содержащие знаков импликации и эквиваленции, равносильны, то и двойственные им формулы также равносильны.

Вопросы для контроля:

1. Равносильные предложения. Равносильные формулы.

2. Свойства отношения равносильности.

3. Равносильные преобразования.

4. Упрощение формул.

5. Применение равносильных преобразований.

6. Принцип двойственности.

Раздел 3. Нормальные формы для формул алгебры высказываний

Дата добавления: 2014-01-06